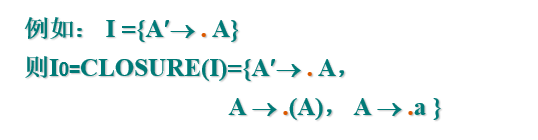语法分析——自底向上分析

**自底向上的语法分析需要解决的关键问题是：如何确定可归约串（即可以归约的字符串）以及每个可归约串用哪个产生式左部的非终结符来归约？针对这些问题的不同解决方法，本章将描述以下两类分析算法：算法优先分析法和LR分析法。其中，LR分析法在目前编译程序中的应用最为广泛，它包括一组分析能力不同的四个算法，按照分析能力从弱到强分别是：LR（0）、SLR（1）、LALR（1）和LR（1）。 **

自底向上的语法分析概述

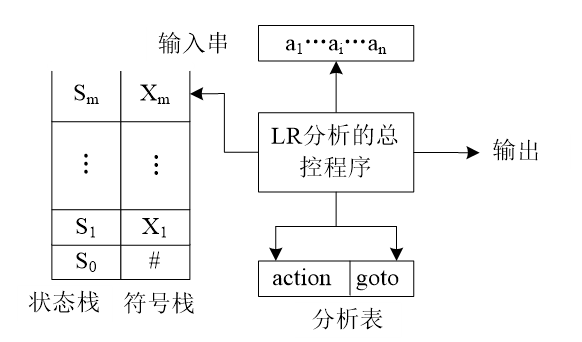
自底向上语法分析器的体系结构

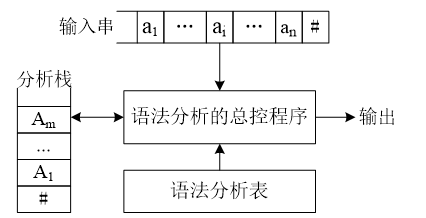
它主要包括四个组成部分：待分析的输入符号串、分析栈、语法分析总控程序以及语法分析表。

在自底向上的语法分析过程中，语法分析的总控程序从左向右地逐个扫描输入字符，根据栈顶元素A和输入符号a所构成的二元组<A，a>查语法分析表，以执行不同的分析动作。其分析动作一共有四种，分别如下：

1. 移进：把输入串的当前符号a压入栈顶，并把指针指向下一个输入符号；
2. 归约：把自栈顶A向下的若干个符号用某个产生式左端的非终结符替换；
3. 接受：表示语法分析成功，此时分析栈的指针指向栈内的唯一符号（即文法的开始符号），输入串指针指向结束符号#；
4. 出错：发现源程序有语法错，调用出错处理程序。

自底向上分析的归约过程

例：

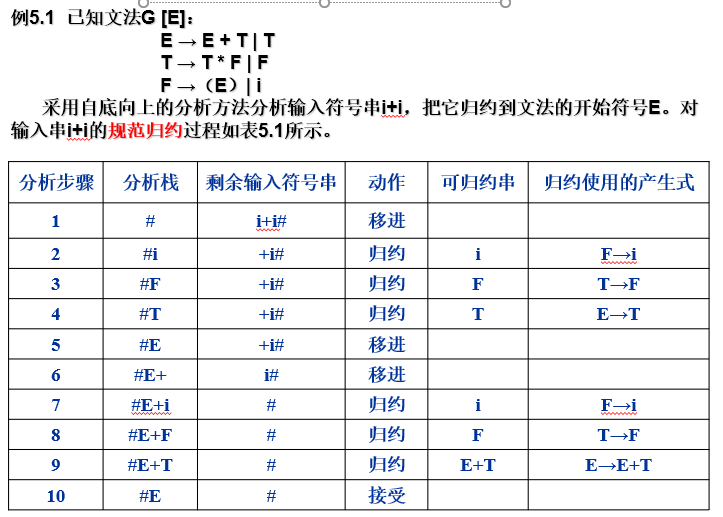
实际上，规范归约过程是最右推导的逆过程，从表5.1可以看出，表中从下往上的六个归约正好对应了最右推导（规范推导）的六个步骤

$E \Rightarrow E+T \Rightarrow E+F \Rightarrow E+i \Rightarrow T+i \Rightarrow F+i \Rightarrow i+i$

显然，该语法分析过程还可以用一棵语法分析树表示出来。

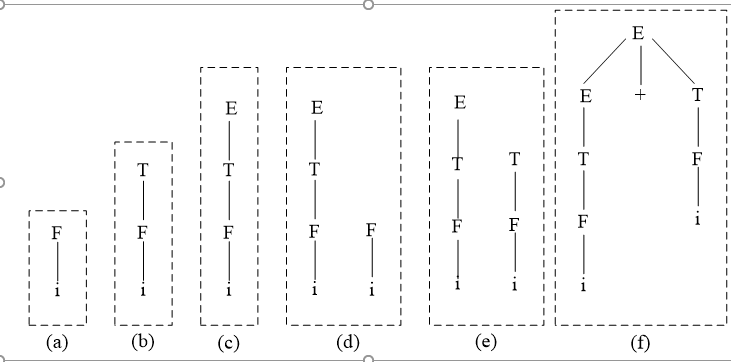
LR分析法

LR分析法概述

1. LR分析法是一类分析方法的简称，通常记为LR(k)分析法
   1. L是指从左至右方式扫描输入串；
   2. R是指最右推导(规范推导)的逆过程；
   3. K是指每次根据当前输入符号最多向前查看K个符号就可以确定下一步动作；
2. 本章重点介绍LR(0) 分析表的构造算法及相关知识。

规范归约（最左归约一最右推导的逆过程）的关键问题是寻找句柄。在一般的“移进-归约”过程中，当一串貌似句柄的符号串出现在栈顶时，用什么方法来判断它是否为一个真正的句柄呢?

LR方法的基本思想是，在规范归约过程中，一方面记住已移进和归约出的整个符号串，即记住“历史”，另一方面根据所用的产生式推测未来可能碰到的输入符号，即对未来进行“展望”。当一串貌似句柄的符号串呈现于分析栈的顶端时，我们希望能够根据所记载的“历史”和“展望”以及“现实”的输入符号等三方面的材料，来确定栈顶的符号串是否构成相对某一产生式的句柄

1. LR(k)分析器的结构

   1. 分析栈（含状态栈和符号栈）
   2. 总控程序（也称为驱动程序）
   3. 分析表（分析动作表和状态转换表）

   

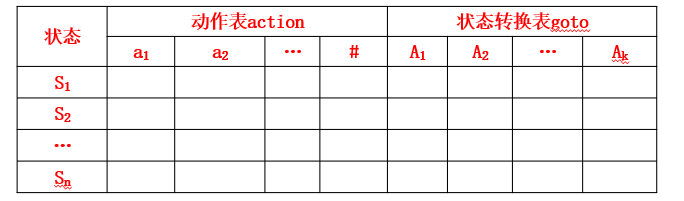
2. LR分析表构成

   LR分析表是LR分析器的核心部分,它由两张表组成:一是动作表(即action表);二是状态转换表(即goto表),见表5.6。表中的$S_1,S_2,…, S_n$为分析器的各个状态；$a_1,a_2,…,a_m$为文法的全部终结符号及右界符’#’；$A_1,A_2,…,A_k$为文法的非终结符号。

   

   在action表中，$action[S_i,a_j]$（即$S_i$所在的行与$a_j$所在的列对应的单元）表示当分析状态栈的栈顶为$S_i$，输入符号为$a_j$时应执行的动作。

   在goto表中，$goto[S_i,A_j]$（即$S_i$行$A_j$列对应的单元）表示当前状态为$S_i$而符号栈顶为非终结符号$A_j$后应移入状态栈的状态。

   action表的动作有以下4种:

   1. 移进($S_m$)。将输入符号$a_j$移进符号栈,将状态m移进状态栈,输入指针指向下一个输入符号。
   2. 归约($r_j$)。当栈顶形成句柄时,按照第j条产生式（如U→ω）进行归约。若产生式右部ω的长度为x,则将符号栈栈顶x个符号和状态栈栈顶x个状态出栈,然后将归约后的文法非终结符号U移入符号栈,并根据此时状态栈顶的状态$S_i$及符号栈顶的符号U,查goto表,将$goto[S_i,U]$移入状态栈。
   3. 接受(acc)。当输入符号串到达右界符’#‘时,且符号栈只有文法的开始符号时,则宣布分析成功,接受输入符号串。
   4. 报错(Error)。当状态栈顶的状态为$S_i$时,如果输入符号为不应该遇到的符号时,即$action[S_i,a_j]$=空白,则报错,调用出错处理程序。

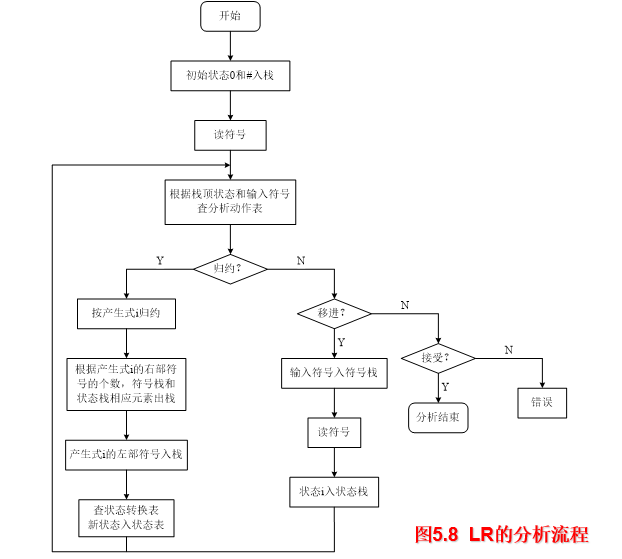
3. LR分析步骤

   1. 将初始状态0、句子的左界符#分别进状态栈和符号栈。

   2. 从输入串中读入当前输入符a，然后由状态栈栈顶元素i与当前输入字符a查action表，决定应取何种动作。

      若$action[i,a]=s_j$，则将状态j及相应的输入符a分别移入状态栈和符号栈栈顶。

      若$action[i,a]=r_j$，则按第j个生产式A→β右部符号β的长度t分别将符号栈、状态栈栈顶t个元素上托出栈，将归约后的A移入符号栈。据此时状态栈栈顶元素 i与归约后的非终结符A，查goto表的[i，A]项，设得到状态j，则将状态j移入状态栈栈顶。

      若为action[i,a]=acc，则结束分析，输入串被接受。

      否则转错误处理程序。

   3. 重复2的工作，直到接受或出错为止。

   

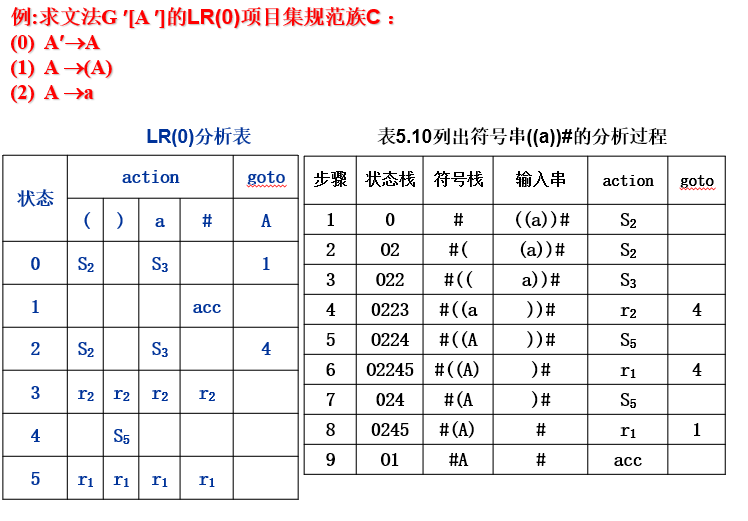
例：

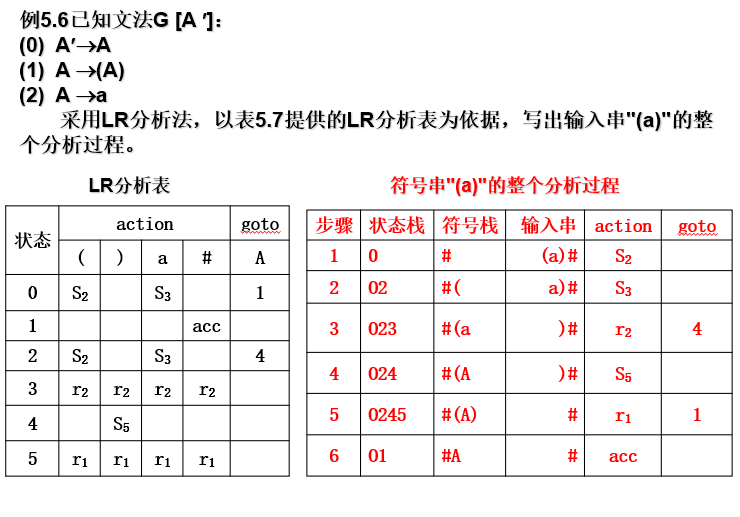
LR(0)分析器

**拓广文法 **

给定文法G，S是其开始符号，G的拓广文法是G，其开始符号为S，区别在于后者仅增加一个产生式$S’ \rightarrow S$,把它作为第0个产生式添加到文法G中。 例如：文法G[A]: $A \rightarrow (A) , A \rightarrow a$ 则该文法的拓广文法G ‘[A ‘]：

$A’ \rightarrow A， A \rightarrow (A)，A \rightarrow a $

1. 活前缀与可规前缀

   自下而上的移进——规约分析，是对句柄进行规范规约，它是规范推导的逆过程，规范推导出来的句型是规范句型。一个符号串的前缀是指该串的任意首部，包括$\varepsilon$。

   对于一个规范句型来说,其活前缀定义如下:

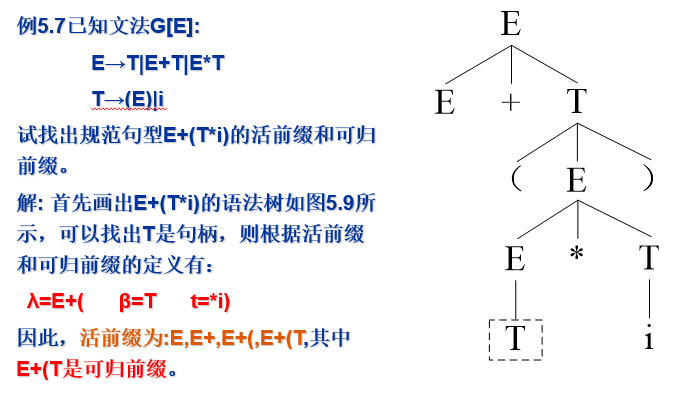
   设λβt是一个规范句型,即λβt是能用最右推导得到的句型,其中β表示句柄,$t∈V_T^*$ ,如果$λβ= u_1u_2…u_r$,那么称符号串$u_1u_2…u_i$(其中l≤i≤r)是句型λβt的活前缀。

   从活前缀的定义可知,一个规范句型的活前缀可以有多个,但观察这些活前缀,会发现其中活前缀$u_1,u_1u_2, u_1u_2…u_{r-1}$不含有完整句柄β,只有活前缀$u_1u_2…u_r$含有完整句柄β,那么这个含有句柄的活前缀$u_1u_2…u_r$称为可归前缀,是最长的活前缀。

   从上述定义可知，活前缀不含句柄右边的任意符号,而可归前缀是含有句柄的活前缀。对一个规范句型来说，活前缀可有多个,可归前缀只有一个。

   例：

   

2. LR(0)项目

   定义：在文法G的每一个产生式右部的某个位置添加一个“·”，点号左边表示该产生式的右部在符号栈的栈顶已经出现的部分，点号右边表示如果要用该产生式进行规约，还应该出现的部分。

   一般产生式$A\rightarrow β$对应的项目个数为| β |+1，特别地，产生式$A \rightarrow ε$的项目个数为1，即$A\rightarrow .$

   $A \rightarrow ·AB $ 希望看到从输入串中与AB对应的符号串。

   $A \rightarrow A·B $ 已识别出由A对应的输入符号，并希望看到与B对应的输入串。

   $A \rightarrow AB· $ 与AB对应的输入串已经识别出来，可以进行规约

项目的分类

不同的项目反映了分析过程中栈顶的不同情况，因此我们可以根据它们的不同作用，将一个文法的全部L(0)项目进行分类：

1. 对于形如$A\rightarrow α·$ 项目，因为它表示右部符号串α(可为ε)已经出现在栈顶，此时相应的动作应该是按此产生式进行归约，故将此项目称为归约项目。

2. 项目$S’ \rightarrow S·$仅用于分析过程中最后一次归约，所以称为接受项目。

3. 对于形如$A\rightarrow α· Xβ$的项目，其中α可以为空符号串：

   当X为终结符号时，相应的分析动作应该将当前的输入符号移入栈中，我们称它为移进项目；

   当X为非终结符号时，由于我们期待着从余留的输入串中进行归约而得到X，因此此类项目为待约项目；

   注： 有的书上还把$S’ \rightarrow · S$称为开始项目，也可称为待约项目

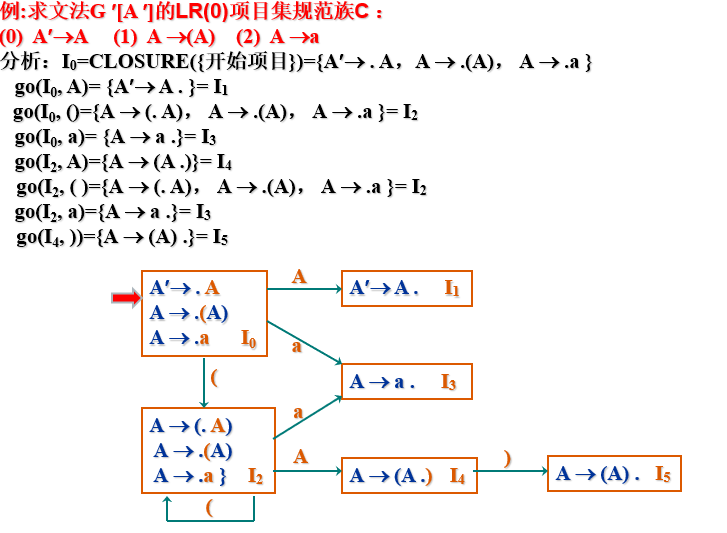
例：

LR(0)项目集规范族的构造

1. 项目集的闭包运算

   设I为项目集（即由项目组成的集合），构造I的闭包函数CLOSURE(I)的算法如下

   1. I中的每一基本项目都属于它；
   2. 若$A\rightarrow \alpha ·B \beta$属于CLOSURE(I)，且$B\rightarrow \gamma$是文法中的一个产生式，则关于非终结符B的任何形如$B\rightarrow· \gamma$的项目也属于它；
   3. 重复上述步骤，直到它不再增大为止

   

2. 项目集之间的转换函数go

   设$I_i$是文法的G[S]的一个LR(0)项目集，非空符号$X \in V_T∪V_N$，定义$I_i$及X间的函数为

   $go(I_i, X)=CLOSURE (J) =I_J$

   其中$J={A\rightarrow \alpha X·\beta \in A\rightarrow \alpha·X \beta \in I_i}$

   1. 先找出Ii中所有形如$A\rightarrow \alpha·X \beta$的项目；
   2. 然后将它们变成$A\rightarrow \alpha X·\beta$放入集合J中；
   3. 再求CLOSURE (J)；

   

LR(0)项目集规范族的构造方法

要构造识别所有规范句型全部活前缀的DFA，首先要确定DFA的状态，而每一个状态都是由若干个LR(0)项目组成的集合，称为项目集。对于构成识别一个文法活前缀的DFA的项目集的全体，称为这个文法的LR(0)项目集规范族（ 即DFA的所有状态）

对于LR(0)项目集规范族——在CLOSURE(I)和go(Ii, X)作用下，可获得的项目集的全体C

1. 令$C={I_0}$ ，其中$I_0=CLOSURE$({开始项目，如$S’\rightarrow ·S$})
2. 对每个$I_i\in C$和$I_i$中形如“· X”的项目，若$go(I_i, X)$非空且不属于C，则将$go(I_i, X)$之值加入C
3. 重复2直至C不再增大

构造识别所有规范句型全部活前缀的DFA

方法：

1. 把文法的LR(0)项目集规范族中的每一个项目集作为DFA的一个状态；
2. 把含有开始项目的项目集作为DFA的初态；
3. 每一个项目集都是DFA的终态；
4. 把文法的终结符和非终结符作为DFA的字母表；
5. $go(I_i, X)$作为单值转换函数

构造LR(0)分析表的算法

1. 若项目$A \rightarrow \alpha ·x \beta \in I_i$ ，且$go(I_i, x)=I_j$

   若$x \in V_T$ ，则置$ACTION[i , x]= S_j$

   若$x \in V_N $，则置GOTO[i, x]=j。

2. 若项目$A \rightarrow \alpha ·\in I_i$,对于任何输入符号$a\in (V_T∪{#})$,则置$ACTION[i,a]=r_j$,即“用第j条产生式$A \rightarrow \alpha $进行归约”（这里假定 $ A \rightarrow \alpha $ 是G’中的第j条产生式）

3. 若项目$S’ \rightarrow S· \in I_k $，则置ACTION[ k , # ]=acc

4. 分析表中凡不能用规则1~3填入信息的元素均置上ERROR（用空白表示）

​ 可以通过识别活前缀的DFA来构造LR(0)分析表

LR（0）分析器的工作过程

分析表是LR分析的关键，有了分析表后就可以在总控程序的控制下对输入符号串进行分析，其分析如下：

1. $action[S,a]=S_j$, S为状态，a为终结符，则把a移入符号栈，状态j移入状态栈
2. 若$action[S,a]=r_j$,a为终结符或’#’,则用第j个产生式归纳约；设k为第j个产生式右部的符号 长度，将符号栈和状态栈顶的k个元素出栈，将产生式左部符号入符号栈；
3. 若action[S,a]=“acc”，a为’#’,则为接受，表示分析成功
4. 若goto[S,A]=j，A为非终结符号并且是符号栈的栈顶，表示前一个动作是归约，A是归约后移入符号栈的非终结符，则将状态j移入状态栈
5. 若action[S，a]=空白，则转入错误处理。

构造LR(0)分析表的步骤小结

1. 写出给定文法G的拓广文法G；
2. 写出文法G的基本LR(0)项目——G’的LR(0)项目集；
3. 利用CLOSURE和go函数，求出相应的LR(0)项目集规范族C；
4. 构造识别该文法全部活前缀的DFA
5. 根据算法构造LR(0)分析表。

语法分析(2)——SLR(1)分析方法

观察上面的项目集会发现$I_1、I_2$和$I_9$，都存在“移进-归约”冲突。比如项目集I2包含两个项目，其中项目E→T·是归约项目，而另外一个项目E→T·*F是移进项目。故，该文法不是LR（0）文法。

按照LR（0）分析表的构造方法可得到分析表见表。

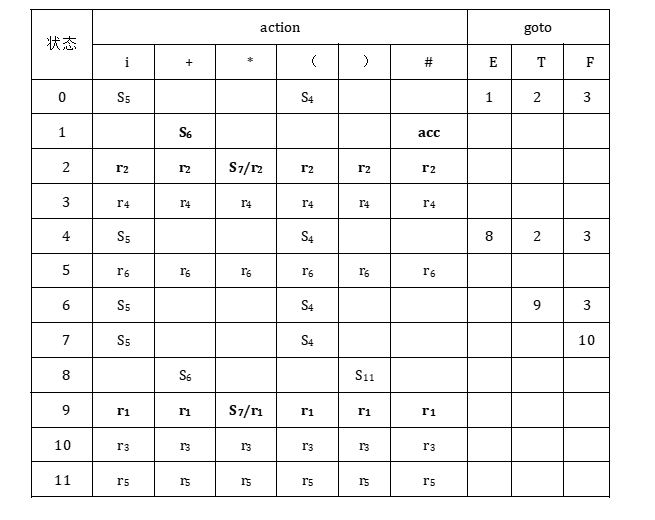
LR(0)文法

如果文法G’的项目集规范族的每个项目集中不存在下述任何冲突项目：

1. 移进项目和归约项目并存；
2. 多个归约项目并存；

则称文法G’为LR(0)文法。

例：

SLR(1)分析法

例：文法G(S)的LR(0)项目集规范族中有这样一个项目集：

$I_3={X\rightarrow \alpha · b \beta， A \rightarrow \alpha · ，B \rightarrow \alpha · }$

且假设$go(I_3, b)=I_4 $

1. $A \rightarrow \alpha$
2. $B \rightarrow \alpha$

分析：由LR(0)项目集规范族构造LR(0)分析表的算法有：

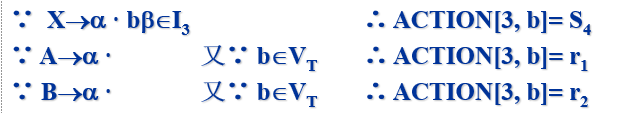
所以 $ACTION[3, b]= S_4$或$r_1$或$r_2$是多重定义元素，故该分析表不是LR(0)分析表，该文法也不是LR(0)文法。

当文法的LR(0)项目集规范族中的项目集出现冲突时，就不能采用LR(0)分析法。实际上，在通过文法的LR(0)项目集规范族构造LR(0)分析表时，若项目$A \rightarrow \alpha.\in I_i$,对于任何输入符号$a\in (V_T∪{#})$,都置$ACTION[i,a]=r_j$,即“用第j条产生式$A\rightarrow \alpha$进行归约”。也就是当$\alpha$在符号分析栈顶部时，我们就进行归约，此时我们根本就不管下一个输入符号是什么。

当然我们还有其他的分析方法，就是在不改变文法的LR(0)项目集规范族的前提条件下，采用向前看一个输入符号的方法来解决项目集中的冲突(即SLR(1)分析法).只不过虽然允许项目冲突，但此时对于项目集中的项目，还有其它的要求

比如在LR（0）项目集规范族中有这样一个项目集：

$I={X \rightarrow \alpha · b \beta， A \rightarrow \alpha · ，B \rightarrow \alpha · }$

1. 对于归约项目：

   $A \rightarrow \alpha · ，B \rightarrow \alpha · $

   求FOLLOW(A), FOLLOW(B)

2. 对于移进项目：

   $X \rightarrow \alpha · b \beta$

   求FIRST($b\beta$)

如果这三个集合存在下列关系：

$FOLLOW(A)∩FOLLOW(B)∩ FIRST(b\beta)= φ $

则通过向前看一个输入符号，移进或归约动作便可唯一确定，即可采用采用SLR(1)分析法。

SLR(1)分析法解决LR(0)项目冲突

1. 设LR(0)项目集规范族的某个项目集I中含有i个移进项目$A_i\rightarrow \alpha.a_i \beta _i$和j个归约项目$B_j\rightarrow \alpha$·

2. 若已知集合{$a_1, a_2, …，a_i$}, $FOLLOW(B_1)$, …, $FOLLOW(B_j)$两两不相交，则I中的冲突动作可通过查看当前输入符号a属于上述j+1个集合中的哪一个集合而获得解决，即

   1. 若$a\in {a_1,a_2, …,a_i}$，则移进a；
   2. 若$a\in FOLLOW(B_k)$，k=1,2, …, j，则用产生式$B_k\rightarrow \alpha$进行归约
   3. 其它则报错

   这种解决动作冲突的办法称为SLR(1)分析法

SLR分析表的构造

构造SLR(1)分析表的方法：

1. **若项目[$A\rightarrow \alpha·X \beta$]$\in I_i$且$goto(I_i, X)=I_j$ **

   若X为终结符，则置$ACTION[i,X]= s_j$；

   若X为非终结符，则置GOTO[i,A]=j ；

2. 若项目$[A \rightarrow \alpha·] \in I_i$则对所有a(或#)$\in FOLLOW(A)$，置$ACTION[i,a]= r_k$ ；

3. 若项目$[S’ \rightarrow S·]\in I_i$，则置ACTION[i,#]= acc；

4. 分析表中凡没有由步骤1至3所定义的表项都置上ERROR（用空白表示）

如果用上述方法构造的分析表无多重定义元素，则称该分析表为SLR(1)分析表，相应的文法称为SLR(1)文法。

现在按照SLR（1）分析表的构造方法，可以得到SLR（1）分析表，如图1所示。注意与表2比较，从而找出与LR(0)分析表的构造方法的不同点

图1：

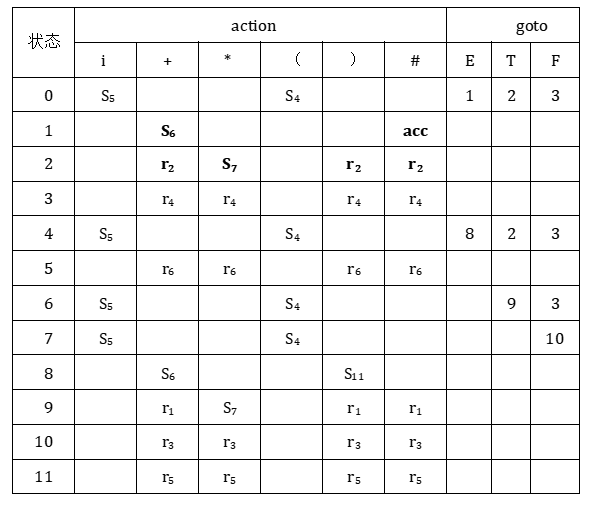
图2：

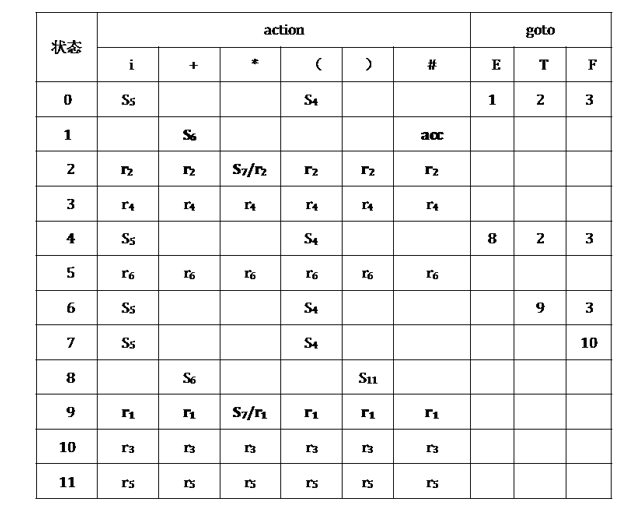
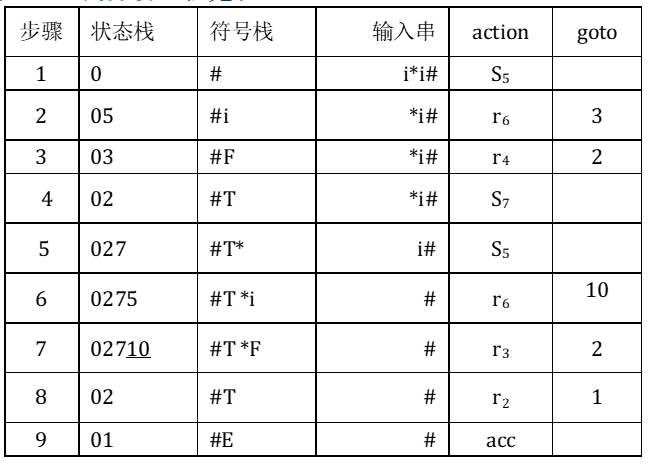
虽然SLR（1）与LR（0）的分析表构造方法略有不同，但它们的分析器的工作过程却完全一样。利用表1分析符号串″i *i#″的分析过程见表3。

例：考虑文法G(S’):

0 $S’\rightarrow S$

1 $S \rightarrow (S)S$

2 $S \rightarrow ε $

分析：

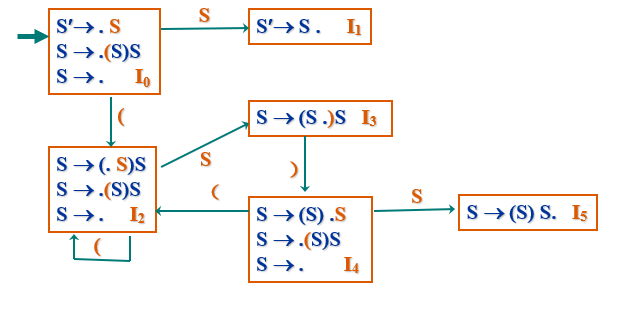
1. 构造识别该文法的所有规范句型的活前缀的DFA，如下图所示

   

2. 对归约项目左部符号求FOLLOW集，有FOLLOW(S)={ ） ，# }

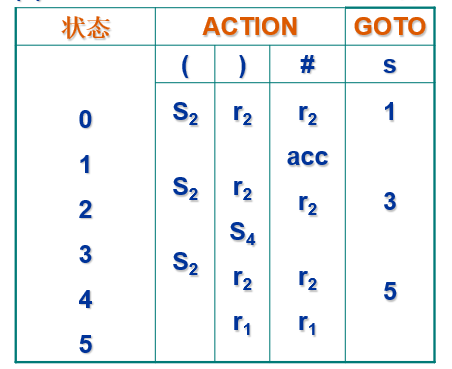
3. 根据SLR(1)分析表的构造方法，由它的DFA得到分析表如下

   

同一个DFA，在构造LR(0)分析表和SLR(1)分析表，主要的区别在于：对于归约项目的动作，一个不需要考虑下一个输入符号，而另一个不需要。