文章 标签 分类

Contents

编译引论(第四章)

 included in 编译原理
   4712 words   10 minutes 

语法分析——自顶向下分析

按照语法分析树的建立方法，可将语法分析方法分成自顶向下和自底向上两大类。

  1. 自顶向下分析方法：语法分析从顶部（树根、语言的识别符号）到底部（叶子、语言的终结符号）为输入的单词符号串建立语法分析树。本章将介绍的递归下降分析方法和LL分析方法就属于自顶向下分析方法。
  2. 自底向上分析方法：语法分析从底部到顶部为输入的单词符号串建立语法分析树。最常见的自底向上分析方法有算符优先分析法和LR分析方法，该部分内容将在第5章介绍。

注：无论采用哪种分析方法，语法分析都是自左向右读入符号

自顶向下分析面临的问题

所谓自顶向下分析方法就是从文法的开始符号出发，按最左推导方式向下推导，试图推出要分析的输入串。它的宗旨是，对任何输入串，试图用一切可能的办法，从文法开始符号出发，自上而下，从左到右地为输入串建立分析树。或者说，为输入串寻找最左推导。这种分析过程本质上是一种试探过程，是反复使用不同的产生式谋求匹配输入串的过程。

例：

若有文法

G[S]: S→aAb

A→cf│c

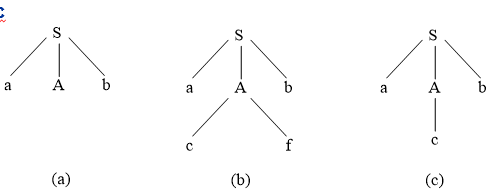
  1. 为了自顶向下地为输入串ω=acb建立分析树，首先建立只有标记为S的单个结点树，输入指针指向ω第一个符号a，然后用S的第一个候选式来扩展该树，得到的树如图（a）所示。

  2. 最左边的叶子标记为a，匹配ω的第一个符号。于是，推进输入指针到ω的第二个符号c，并考虑分析树上的下一个叶子A，它是非终结符。

    用A的第一个候选式来扩展A，得到图（b）的树。现在第二个输入符号c能匹配，再推进输入指针到b，把它和分析树上的下一个叶子f比较。因为b和f不匹配，回到A，看它是否还有别的候选式尚未尝试。

  3. 在回到A时，必须重置输入指针于第二个符号，即第一次进入A的位置。现在尝试A的第二个选择，得到图（c）的分析树。叶子c匹配ω的第二个符号，叶子b匹配ω的第三个符号。这样，得到了ω的分析树，从而宣告分析完全成功

https://cdn.jsdelivr.net/gh/adan-ning/images/202404031647084.png

自顶向下分析面临的问题

自顶向下分析法存在困难和缺点：

  1. 首先，如果存在非终结符A，并且有A Aa这样的左递归，那么文法将使上述自顶向下分析过程陷入无限循环。因为当试图用A去匹配输入串时会发现，在没有吃进任何输入符号的情况下，又得要求用下一个A去进行新的匹配。因此，使用自上而下分析法时，文法应该没有左递归。
  2. 其次，当非终结符用某个选择匹配成功时，这种成功可能仅是暂时的。由于这种虚假现象，需要使用复杂的回溯技术。由于回溯，需要把已做的一些语义工作（如中间代码的生成等）推倒重来。这些事情既麻烦又费时间，所以最好设法消除回溯。同时，回溯使得分析器难以报告输入符号串出错的确切位置。
  3. 最后，试探与回溯是一种穷尽一切可能的办法，效率低，代价高，它只有理论意义，在实践中的价值不大。

LL（1）文法

FIRST集（首符号集）

定义：设 G[S] = (VT ,VN , S , P) 是上下文无关文法，则

$FIRST(x) = {a|x \stackrel{}\Rightarrow ay,a∈ VT,x,y ∈ V}$

若$x \stackrel{*} \Rightarrow ε$，则规定ε∈FIRST(x)

实际上， FIRST(x)是指由符号串x出发能够推导出来的所有符号串中，处于串头的终结符号的集合。

**FIRST(X)可按以下算法求得： **

设：X=X1X2…Xn，FIRST(X)=Φ，i=1则有：

  1. 若$X_i∈V_T$,则$X_i∈FIRST(X)$,进入第4步;
  2. 若$X_i∈V_N$,
    1. 若$X_i \stackrel{*} \nRightarrow ε$,则FIRST(Xi)∈FIRST(X),进入第4步;
    2. 若$Xi \stackrel{*} \Rightarrow ε,则FIRST(Xi)\ ε∈FIRST(X)$,然后令i=i+1,若i≤n，进入第1步,否则进入第3步；
  3. 若 $X \stackrel{*} \Rightarrow ε$，则ε∈FIRST(X)；
  4. 退出

例：

已知文法G[E]：

	E→TE'
	E'→+TE'|ε
	T→FT'
	T'→*FT'|ε
	F→(E)|i

求文法中的非终结符号以及符号串TE’、+TE’、ε、FT’的FIRST集

解：首先，求各非终结符号FIRST集：

https://cdn.jsdelivr.net/gh/adan-ning/images/202404031700741.png

FOLLOW集（后继符号集）

定义：设 $G[S] = (V_T ,V_N , S , P)$ 是上下文无关文法，$A∈V_N$ , 则

$FOLLOW(A)={a|S \stackrel{*} \Rightarrow …Aa… ,a∈V_T}$

若$S \stackrel{*} \Rightarrow …A$，则规定 #∈FOLLOW(A)

实际上， FOLLOW(A)是指文法G[S] 的所有句型中，紧跟在非终结符A后的终结符号的集合。

#作为输入串的结束符，或称为句子括号，如：abc#

FOLLOW(A)可采用以下算法求得：

  1. 对于文法G[S]的开始符号S，有#∈FOLLOW(S)；

  2. 若文法G[S]中有形如U→xA的规则,其中x∈V﹡,则

    FOLLOW(U)∈FOLLOW(A)

  3. 若文法G[S]中有形如U→xAy的规则,其中x∈V﹡,y∈V﹡,

    1. 当$y \stackrel{*} \nRightarrow ε$时, FIRST(y)∈FOLLOW(A)
    2. 当$y \stackrel{*} \Rightarrow ε$时, FIRST(y)\ ε∈FOLLOW(A) FOLLOW(U)∈FOLLOW(A)

例：

已知文法G[E]：

E→TE'
E'→+TE'|ε
T→FT'
T'→*FT'|ε
F→(E)|i

求各非终结符号的FOLLOW集。

https://cdn.jsdelivr.net/gh/adan-ning/images/202404031706587.png

SELECT集（可选集）

定义:给定上下文无关文法的产生式A→x,A∈VN, x∈V*,则

  1. 若$x \stackrel{*} \nRightarrow ε$，则SELECT(A→x)=FIRST(x)
  2. 若$x \stackrel{*} \Rightarrow ε$，则SELECT(A→x)=FIRST(x)\ε∪FOLLOW(A)

实际上SELECT(A→x)是指，在推导过程中，如果采用了A→x进行推导，下一个可能推导出的终结符号。

例：

已知文法G[S]：

S→AB|bC

A→b|ε

B→aD|ε

C→AD|b

D→aS|c

求出符号串AB、bC、ε、AD的FIRST集，非终结符号的FOLLOW，以及所有产生式的SELECT集。

https://cdn.jsdelivr.net/gh/adan-ning/images/202404031709618.png

https://cdn.jsdelivr.net/gh/adan-ning/images/202404031710578.png

LL（1）文法

一个上下文无关文法是LL（1）文法，当且仅当对于每个非终结符A的任何两个候选式A→α|β满足：

SELECT（A→α）∩SELECT（A→β）=∅

其中$A∈V_N，α、β∈V^*$，且不能同时推导出ε。

例：

判断下面的文法是否是LL（1）文法：

https://cdn.jsdelivr.net/gh/adan-ning/images/202404031711688.png

递归下降分析法

递归子程序法也称为递归下降分析法，是一种简单直观易于构造的自顶向下分析方法，其核心思想是：对文法的每一个非终结符号编制一个处理子程序，而处理子程序的代码结构则由相应的非终结符号的规则右部所决定。

也就是说递归下降分析法为文法中的每一个非终结符编写一个递归过程，识别由该非终结符推出的符号串，当某非终结符有多个候选式时，能够按照LL（1）形式确定地选择某个产生式进行推导。用这种方法进行语法分析时，从读入第一个单词开始，由开始符号出发进行分析。若遇到非终结符，则调用相应的处理过程；若遇到终结符，则判断当前读入的单词是否与该终结符相匹配，如果匹配，则读取下一个单词继续分析。

设LL（1）文法$G（V_N，V_T，P,S），V_N={X_1,X_2,…,X_n}$。对文法的每个非终结符号Xi，可以按照以下方法来设计递归下降分析子程序Xi（）：

  1. 对于形如$X_i→γ_1|γ_2|…|γ_m$的产生式，在相应子程序$X_i（）$中，应该能够判断当前输入符号a属于哪个候选式$γ_j$的SELECT集，并转入该候选式相应的代码段，继续识别，对候选式的选择可用if语句或case语句实现。
  2. 对于形如$X_i→Y_1Y_2…Y_k（Y_j∈V_N∪V_T）$的产生式，相应子程序$X_i（）$是一个依次识别其右部各符号$Y_j（j=1,2,…,k）$的过程；如果$Y_j∈V_T$，则判断当前输入符号是否与Yj匹配；若$Y_j∈V_N$，则应调用相应于$Y_j$的子程序的代码。
  3. 对于形如$X_i→ε$的产生式，在相应的子程序$X_i（）$中，应该能够判断当前输入符号a是否属于集合FOLLOW(Xi),从而决定是从$X_i（）$返回还是报错。
  4. 在各个子程序$X_i（）$中，均应含有进行语法检查的代码。

例 下面LL（1）文法产生pascal类型的子集，用dotdot表示“..”，以强调这个字符序列作为一个词法单元。

https://cdn.jsdelivr.net/gh/adan-ning/images/202404121640327.png

规则 type→ simple |↑id |array [simple] of type

该该非终结符对应的递归分析子程序伪代码如下：

    procedure type;
       begin
            if lookahead in {integer,char,num}   then   simple( )
                else if  lookahead=‘↑’  then 
                      	begin
                       		match(‘↑’);
			match(id)
                    	end
            	else if  lookahead=array  then 
		begin
                       		match(array);
			match(‘[’);
			simple( );
			match(‘[');
			match(of);
			type( )
                    	end
            	else  error( )
      end;

变量lookahead来存放向前查看的单词符号。如果lookahead∈SELECT（simple）={integer,char, num}，则转入simple子程序；如果当前单词符号为↑，则调用匹配函数match( )，检查是否匹配，若匹配则读入下一个单词符号，存放到变量looahead 中，然后继续调用match( )，检查当前符号是否与match函数的参数id匹配，若匹配则意味着可以选取产生式type→↑id；如果当前单词为array，则依次执行以下操作：匹配array，匹配“[”，调用simple()，匹配"["，匹配of，调用type( )；如果lookahead中的单词符号不是上述符号，则调用出错处理函数error( )。

规则 simple→integer | char |num dotdot num

该该非终结符对应的递归分析子程序伪代码如下：

procedure  simple；
begin
      if lookahead=integer then 
                                        match(integer)
              else if lookahead=char then 
                                        match(char)
              else if lookahead=num then 
		begin
                      	           match(num)；
                                        match(dotdot)；
                                        match(num)
                      	end
             else  error( )
end；

预测分析法

定义：所谓预测分析法也称为LL(1)分析，是指从左到右扫描输入源程序，同时采用最左推导，且对每次直接推导只需向前查看一个输入符号，便可以确定当前所应选择的规则。

理解：

  1. 第一个L表示：自顶向下分析是从左向右扫描输入串。
  2. 第二个L表示：分析过程中将用最左推导。
  3. 1表示：只需向右看一个符号便可决定如何推导（即选择哪个产生式进行推导）

预测分析器的结构

预测分析器（即实现预测分析法的程序）的结构如图所示

https://cdn.jsdelivr.net/gh/adan-ning/images/202404121645136.png

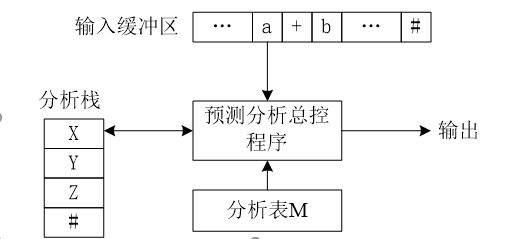
输入缓冲区：用于存放待分析的符号串ω，ω后紧跟边界符#；

分析栈：存放一系列文法符号，边界符#存于栈底。分析开始时，先将#入栈，然后再置入文法开始符号。

预测分析表M：它与文法有关，它是一个二维数组M[A,a]，其中，A是非终结符号，a是终结符号或#，存放非终结符号A对应输入符号a时应该选择的产生式，是预测分析时的主要依据。

输出流：分析过程中所采用的产生式序列。

预测分析总控程序：它是预测分析器的核心，它总是根据栈顶符号X和当前输入符号a来决定分析程序应该采取的动作，有四种可能：

  1. 若X=a≠#，则分析程序从STACK的栈顶弹出终结符号X，输入指针前移一个位置，指向下一个输入符号（即a的后继符号）；
  2. 若X=a=#，则分析程序宣告分析成功，停止分析；
  3. 若$X∈V_T$（即X是终结符号），但X≠a，则分析程序调用出错处理程序，以报告错误。
  4. 若$X∈V_N$（即X是非终结符号），则分析程序访问分析表M[X，a]：
    1. 若M[X，a]的值是X的产生式$X→Y_1Y_2…Y_K$，则先X弹出分析栈，然后把产生式的右部符号串按反序（即$Y_K，…Y_2，Y_1$的顺序）一一压入分析栈。特别的是，若X的产生式的右部是ε(即X→ε)时，则分析程序只需要将X弹出分析栈即可。
    2. 若M[X，a]的值是出错标记error，则分析程序调用出错处理程序，以报告错误。

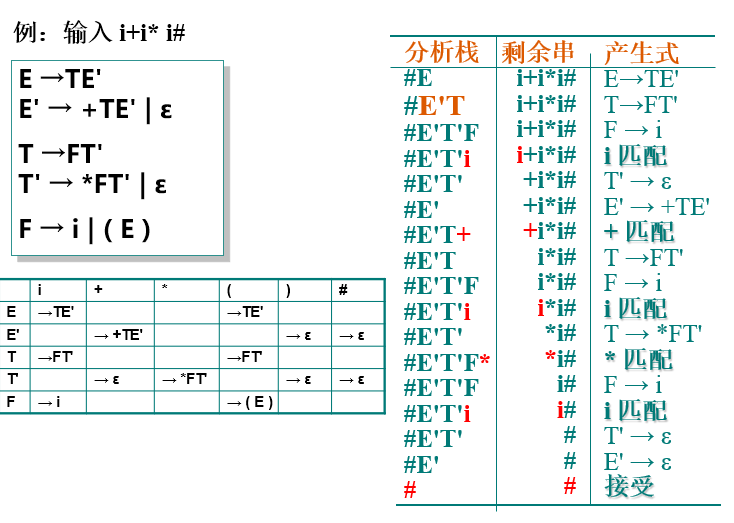
预测分析器的工作过程

https://cdn.jsdelivr.net/gh/adan-ning/images/202404121648860.png

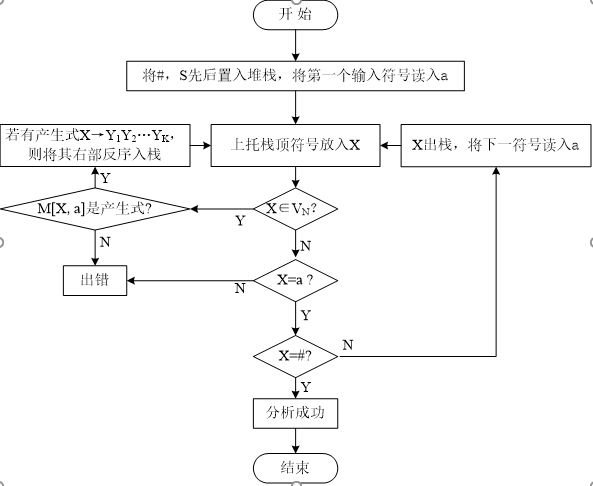
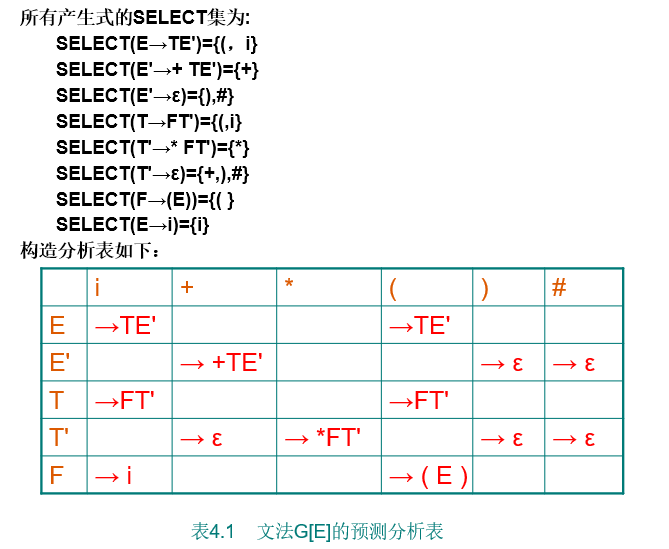
LL(1)分析表的构造

LL(1)分析表M[A,a]实际上是要表明要由A推导出终结符a所应采用的产生式。我们可以利用SELECT集来构造LL(1)分析表，具体构造算法如下：

设有文法$G[S]=(V_N,N_T,P,S), V_N={A_1,A_2,…,A_m}$,令i=1

  1. 若关于$A_i$的规则有： $A_i →x_1|x_2|…|x_n$

    则求的各规则的SELECT集。

  2. 若$a∈ SELECT(A_i→x_j)$,则

    M[Ai ,a]= Ai→xj

  3. i=i+1,重复1、2，直到i>m,即对文法的所有的非终结符号求完为止。

https://cdn.jsdelivr.net/gh/adan-ning/images/202404121652865.png

https://cdn.jsdelivr.net/gh/adan-ning/images/202404121652010.png

https://cdn.jsdelivr.net/gh/adan-ning/images/202404121652844.png

Updated on 2024-04-03
 编译原理
Back | Home