编译引论(第三章)
词法分析
词法分析程序的功能
词法分析程序的主要任务是按语言的词法规则从源程序中逐个识别单词,把字符串形式的源程序转换为单词串的形式,并把每个单词转换成他们的内部表示,即所谓的“TOKEN”,同时进行词法检测
词法分析和语法分析之间的关系通常由两种形式
- 词法分析程序既可作为编译器的独立一遍来完成
- 也可作为词法分析的一个子程序
单词的种类及词法分析的输出
单词符号是一个程序语言的最小语法单位,一般分为5类:
- 保留字。保留字是由程序语言定义的具有固定意义的标识符。有时称这些标识符为关键字或基本字。例如,Pascal中的begin,end,if,while都是保留字。这些字通常不用作一般标识符
- 标识符。用来表示各种名字,如变量名,数组名,过程名等
- 常数。常数的类型一般有整型,实型,布尔型,文字性等。例如,100,3.14159,TRUE,‘Sample’
- 运算符。如+,-,*,/等
- 界符。如逗号,分号,括号,/*,*/等
词法分析器所输出的单词符号通常表示成二元式:(单词类别,单词符号的属性值)
单词类别通常用整数编码。标识符一般统归为一类。常数则宜按类型(整,实,布尔等)分类。关键字可将全体视为一类,也可以一字一类。采用一字一类的分法实际处理起来较为方便。运算符可采用一类的分法,但也可以把具有一定共性的运算符视为一类。至于界符一般用一类的分法
单词符号的属性是指单词符号的特性或特征。属性值则是反应特性或特征的值。例如,对于某个标识符,常将存放它的有关信息的符号表项的指针作为其属性值;对于某个常数,则将存放它的常数表项的指针作为其属性值
词法分析的手工设计
新程序的输入
- 利用词法分析器生成器:此时生成器将提供用于源程序字符流的读入和缓冲的若干子程序
- 利用传统的系统程序设计语言来编写词法分析器:此时要利用该语言所具有的输入/输出能力来处理读入操作
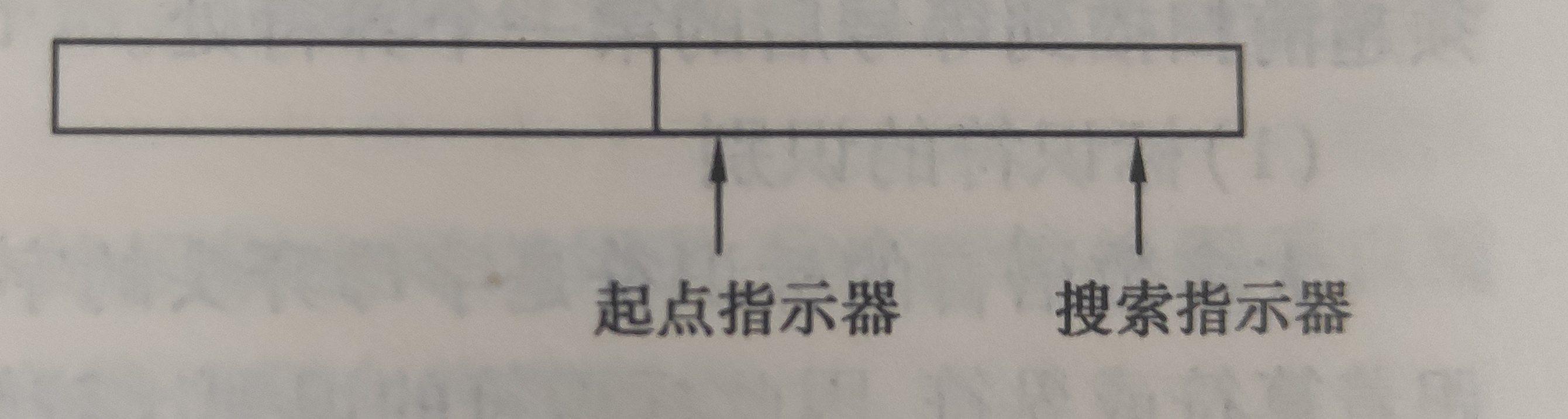
不论扫描缓冲区设得多大都不能保证单词符号不会被它的边界所打断。因此,扫描缓冲区最好是用一个如图所示得一分为二的缓冲区域
单词的识别和超前搜索
有些语言(如FORTRAN)对于保留字不加保护,用户可以用它们作为普通标识符,这就使得保留字的识别相当困难。请看下面两条正确的FORTRAN语言语句:
- DO99K=1,10
- DO99K=1.10
若下一个界符是逗号,则可以肯定DO是保留字,否则,DO不构成保留字,它只是用户标识符的头两个字母,因此,为了区别语句1,2,必须超前扫描到等号后的第一个界符处。
-
标识符的识别
大多数语言的标识符是字母开头的字母和数字组成的串,而且在程序中标识符出现后都跟着算符和界符,因此标识符的识别比较简单
-
常数的识别
大多数语言算数常数的表示大体相似,对于它们的识别比较直接。但对于某些语言的常数的识别也需要用超前搜索的方法。例如,对于FORTRAN语言的语句:
IF(5.EQ.M)I=10
其中,5.EQ.M只有当超前扫描到字母Q时才能断定5的词性。因为5.EO8和5.EQ.M的前三个字符完全一样
-
算符和界符的识别
词法分析器将那些有多个字符复合成的算符和界符(如C语言中的++)拼合成一个单词符号。因为这些字符串是不可分的整体,若分化开来,便失去了原来的意义。在这里同样需要超前搜索
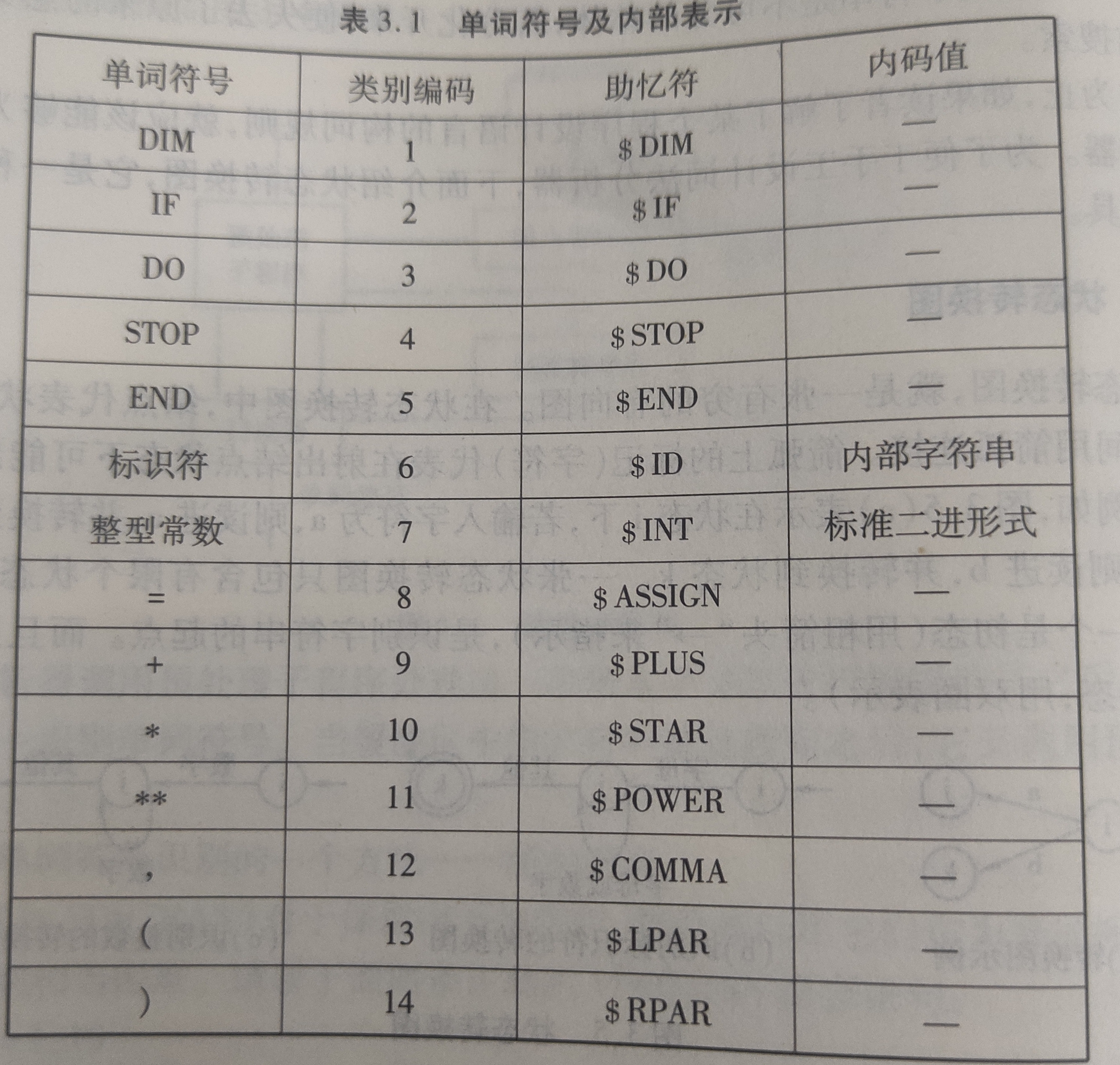
状态转换图
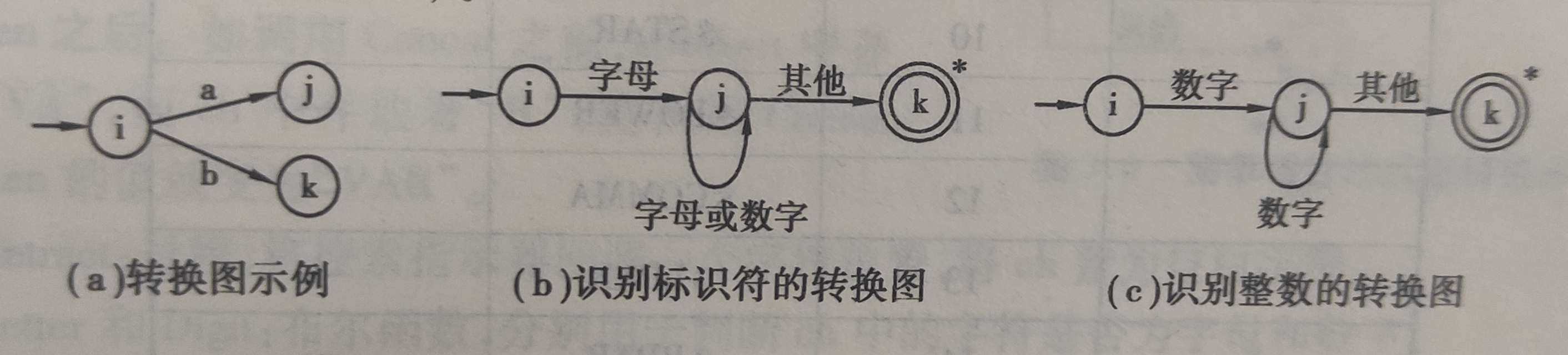
所谓状态转换图,就是一张有穷的有向图。在状态转换图中,结点代表状态,用圆圈表示。状态之间用箭弧连接。箭弧上的标记(字符)代表在射出结点状态下可能出现的合法的输入字符。如图a;
一个状态转换图可用于识别(或接受)一定的字符串,如图b;
如果在状态i时输入字符不为“字母”,则意味着识别不出标识符,或者说这个转换图工作不成功。有如,识别整数的状态转换图如图c所示,其中,i为初态,k为终态。大多数程序语言的单词符号都可以用状态转换图予以识别
注:终态结上打个星号“*”意味着多读进一个不属于标识符部分的字符,应把它退还给输入串
词法分析的手工构造
简单语言的单词符号
状态转换图
单词可分为单字符单词和多字符单词。对于单字符的识别比较简单,见字符即知,如=,+,*等,无须多读,无须退回。对于多字符单词的识别比较麻烦,存在多读,退回处理。一个程序设计语言的单词识别,可以用若干张状态转换图予以描述,也可以用一张状态图转换图来描述。
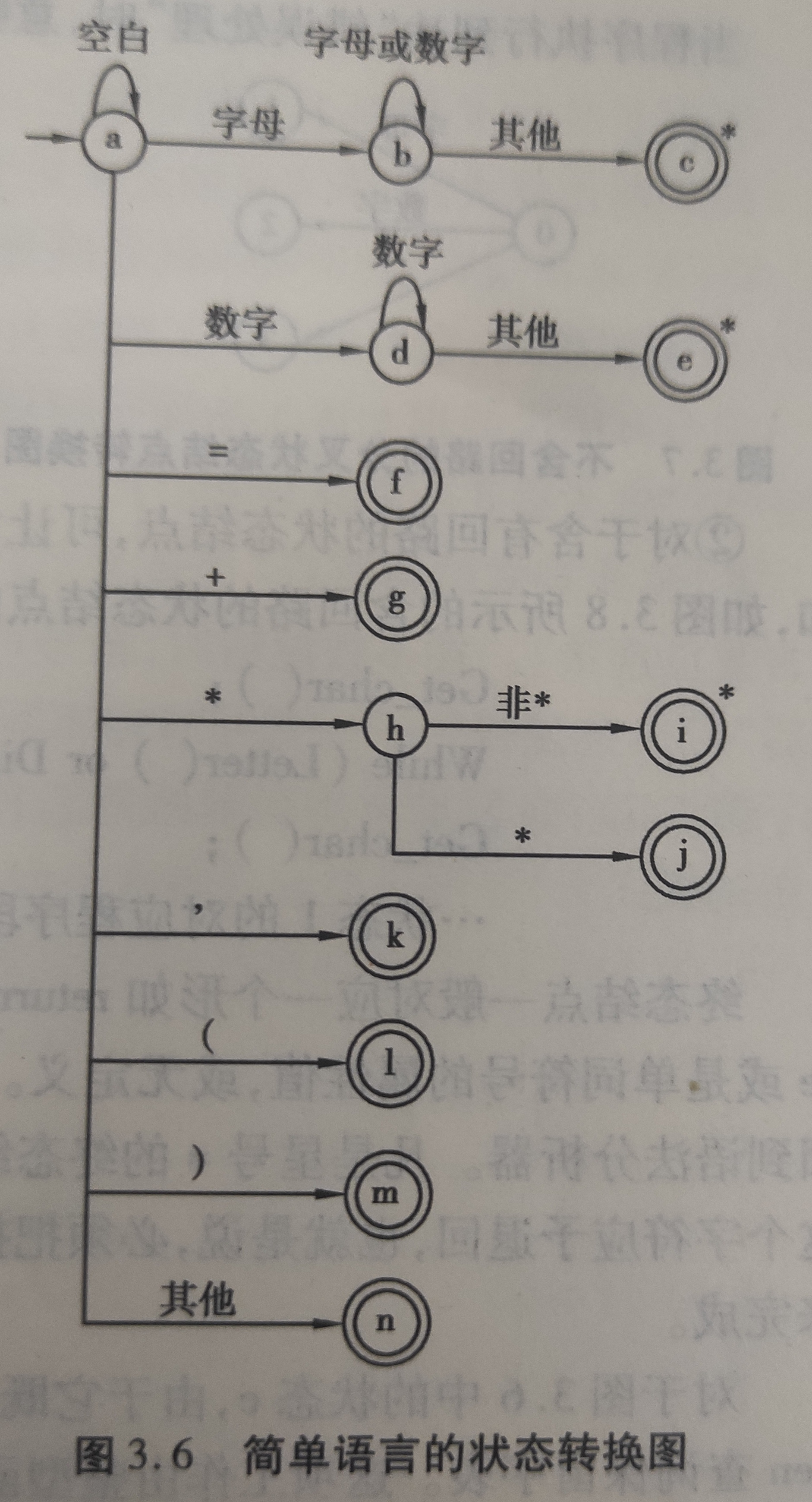
为了把这个例子阐述得更简单,有几点重要限制:
- 所有保留字(如IF,WHILE等)都是“保留字”,用户不得使用它们作为自己定义的标识符,这样就避免了识别保留字时使用超前搜索技术。例如,DO(2)=x这种写法是绝对禁止的
- 把保留字作为一类特殊标识符来处理,对保留字不专门设计对应的状态图。把保留字及其类别编码预先安排在一张表格中(即保留字表)。当状态转换图识别出一个标识符时,就去查保留字表,确定是它是否为保留字。
- 如果保留字,标识符和常数之间没有运算符或界符作间隔时,则必须至少用一个空白符作间隔
在上述限制条件下,多数单词符号的识别就不必使用超前搜索技术。在此,可通过一张状态转换图来识别上图的单词符号,如图所示:
状态转换图的程序实现
用程序实现状态转换图的办法是让每个状态结点对应一段程序
-
设计一组全局变量,过程和函数
- ch:字符变量,存放最新读入的源程序字符
- strtoken:字符数组,存放构成单词符号的字符串
- Get_char:过程,将下一输出字符读到ch中,搜索指示器前一字符位置
- Get_BC:过程,检查ch中的字符是否是空白符,若是,则调用Get_char直到ch中进入一个非空白字符
- Concat:过程,将ch中的字符连接到字符数组strtoken之后。如调用Concat之前,strtoken中存放的是“VA”,而ch中存放着“R”,则调用Concat后,strtoken的值就变为“VAR”
- Retract:过程,将搜索指示器回调一个字符位置,将ch置为空白字符
- Letter和Digit:布尔函数,分别用于判断ch中的字符是否为字母和数字
- Reserve:整型函数,对字符数组strtoken中的字符串查找保留字表,若它是一个保留字则返回它的编码,否则返回0值(假定0不是保留字的编码)
- Insert_Id:整型函数,将字符数组strtoken中的标识符插入符号表,返回符号表指针
- Insert_Const:整型函数,将字符数组strtoken中的常数插入常数表,返回常数表指针
- Error:出错处理
-
状态转换图的具体实现
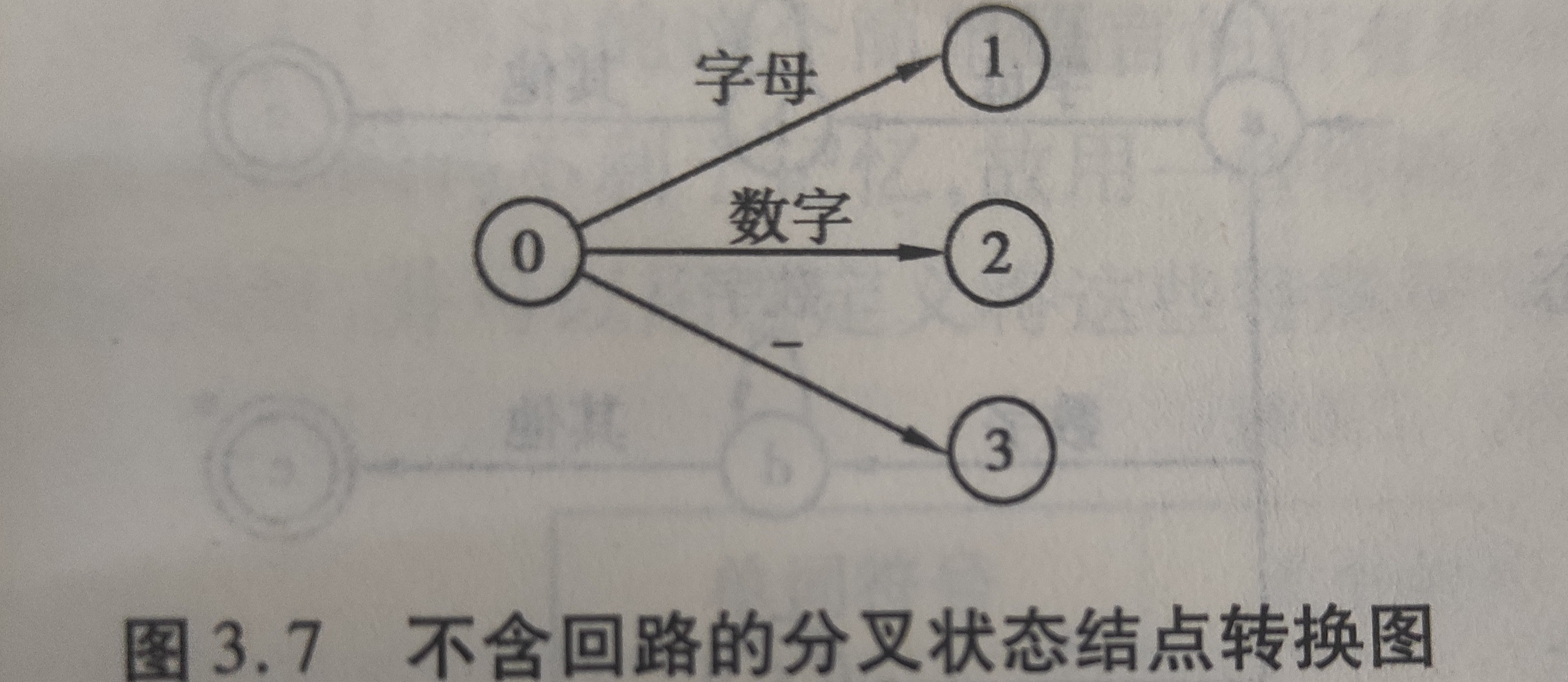
一般来说,构造识别状态转换图的程序,可让每个状态节点对应一段程序。具体实现时,可分为不含回路的分叉状态节点和含回路的状态节点来讨论。
-
对于不含回路的分叉状态结点,可让它对应一个switch语句或一组if…then…else语句
例如,如图所示的不含回路的分叉状态结点的转换图,其状态节点0所对应的程序段可表示为

Get_char(); If(Letter()); {...状态1的对应程序段...;} else if(Digit()) {...状态2的对应程序段...;} else if(ch='_') {...状态3的对应程序段...;} else {...错误处理}
当程序执行达到"错误处理"时,意味着现行状态0和当前所面临的输入串不匹配.
-
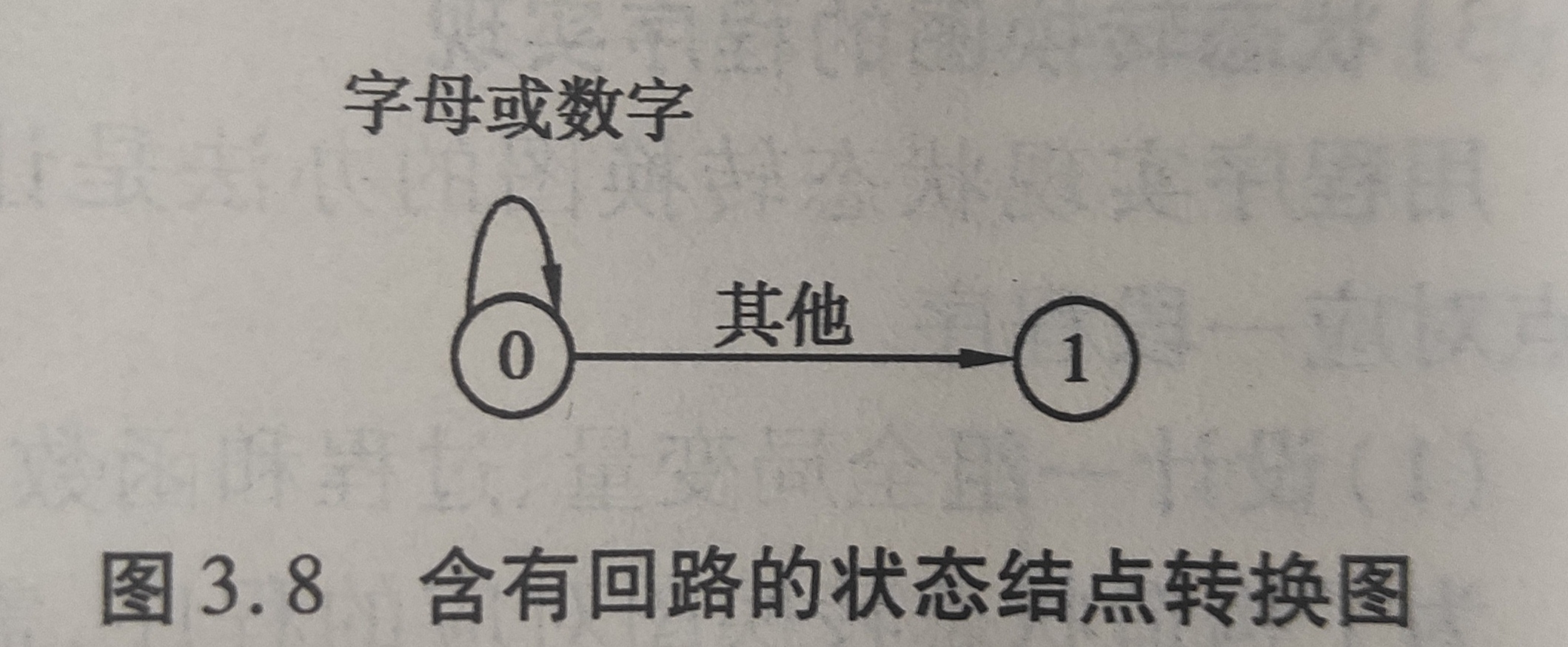
对于含有回路的状态结点,可让它对应一个有while语句的if语句构成的程序段。例如,如图所示的按回路的状态节点的转换图,其状态节点0所对应的程序段可为

Get_char(); While(Letter() or Digit()) Get_char(); ...状态1的对应程序段...对于上图 中的状态c,由于它既是标识符的出口又是保留字的出口,因此,需要对strtoue查询保留字表。这项工作由整型函数过程Reserve来完成。若此过程工作结果所得的值为0,则表示strtoken中的字符串是一个标识符(假定0不是保留字的编码);否则,表示保留字编码。
综上,如图 所示的状态转换图所对应的词法分析器的主题程序如下:
int code,value; strtoken:=" "; /*将strtoken初始化为空串*/ Get_char(); Get_BC(); if(Letter()) begin while(Letter() or Digit()) begin Concat(); Get_char(); end Retract(); code:=Reserve(); if(code = 0) begin vaue:=Insert_Id(strtoken); return($ID,value); end else return(code,-); end else if (Digit()) begin while(Digit()) begin Concat(); Get_char(); end Retract(); value:=Insert_Const(strtoken); return($INT,value); end else if(ch='=') return($ASSIGN,-); else if(ch='+') return($PLUS,-); else if(ch='*') begin Get_char(); if(ch='*') return($POWER,-); Retract(); return($STAR,-); end else if(ch=',') return($COMMA,-); else if(ch='(') return($LPAR,-); else if(ch=')') return($RPAR,-); else Error(); /*错误处理*/
-
正规式与正规集
设字母表为$\sum$,辅助字母表$*\sum = {\varepsilon,\phi,|,\cdot , * ,( , )}$,下面是正则表达式和它所表示的正规集的递归定义:
-
$\varepsilon$和$\phi$都是$\sum$上的正规式,它们所表示的正规集分别为{$\varepsilon$}和$\phi$ ;
-
任何$a \in \sum$,a是$\sum$ 上的一个正规式,它所表示的正规集为{a};
-
假定U和V都是$\sum$上的正规式,它们所表示的正规集分别记为L(U)和L(V),则:
U|V是正规式,它所表示的正规集为L(U)$\cup$L(V);
U$\cdot$V是正规式,它所表示的正规集L(U)L(V)(即连接积)。
$U^$是正规式,它所表示的正规集为$(L(U))^$
仅有有限次使用上述3步骤而得到的表达式才是$\sum$上的正规式。仅有这些正规式所表示的字符集才是$\sum$上的正规集
有限自动机
确定有限自动机
一个确定有限自动机(DFA)M是一个五元式:$M=(S, \sum ,f,s_0,Z)$
- S是一个有限集,它的每个元素称为一个状态
- $\sum$是一个有穷字母表,它的每个元素称为一个输入字符
- f是转换函数,是一个从$S \times \sum$至S的单值映射,f($S_1$,x)=$S_2$意指:当现行状态为$S_1$,面临的输入符号为x时,将转到下一状态$S_2,S_2$称为$S_1$的一个后继状态;
- $S_0 \in S$,它是唯一的一个初态;
- $Z \subseteq S$称为终止状态集(可空)。
一个DFA的转换函数可用一个状态转换矩阵或状态转换表来表示,该矩阵的行表示状态$S_i(S_i∈S)$,列表示输入字符$a_j(a_j∈∑)$,矩阵中的元素则是转换函数$ f (S_i , a_j)$的值。
例:已知DFA M=({A,B,C,D},{x, y}, f ,A,{D})其中f为:
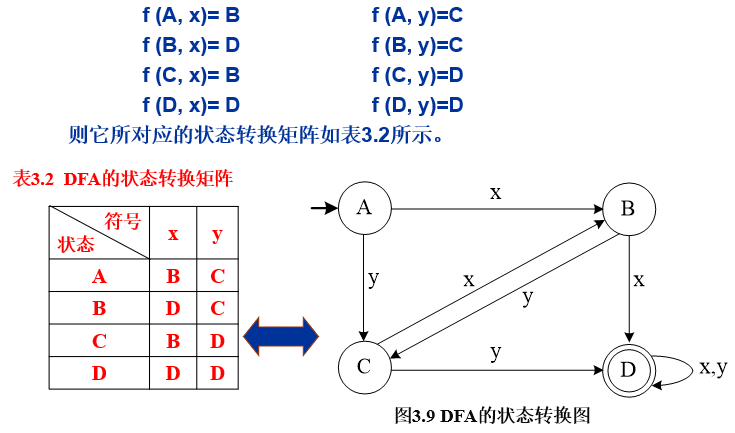
确定有限自动机识别的符号串
对于Σ上的任意符号串$W ∈Σ^*$,若存在一条从初态结点到终态结点的路径,该路径上每条箭弧的标记连接成的符号串恰好是W,则称W为DFA $M_D$所识别。
DFA $M_D$所能识别的符号串的全体记为$L(M_D)$,称为$M_D$所识别的语言。
例:已知自动机的状态转换图如下:
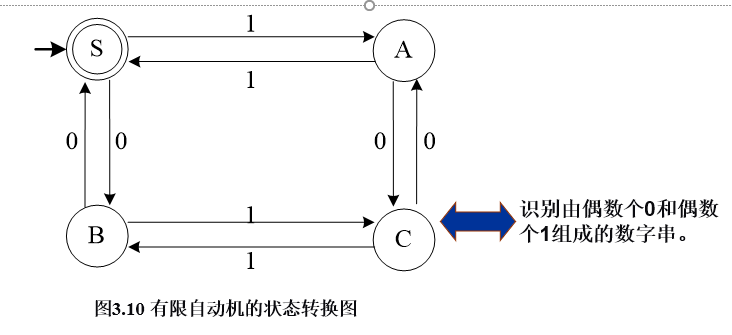
DFA的确定性
DFA的确定性表现在转换函数f:S×∑→S是一个单值函数。也就是说,对任何状态Si∈S和输入符号a∈∑,f (Si ,a) 唯一地确定了下一状态。从状态转换图的角度来看,假定字母表∑含有n个输入字符,那么,任何一个状态结点最多只有n条弧射出,而且每条箭弧以一个不同的输入字符来标记。如果f是一个多值函数,这就涉及到非确定有限自动机的概念。
非确定有限自动机
一个非确定有限自动机(NFA)M是一个五元式:$M=(S, \sum ,f,S_0,Z)$
- S是一个有限集,它的每个元素称为一个状态。
- ∑是一个有穷字母表,它的每个元素称为一个输入字符。
- f是转换函数,是一个从S×Σ* 到S的子集的映射,即f:S×Σ*→2s
- $S_0 \subseteq S$,是一个非空初态集;
- $Z \subseteq S$称为终止状态集(可空)。
和确定有限自动机一样,非确定有限自动机也可以用状态转换图和状态转换矩阵来表示。
显然,一个含有m个状态和n个输入字符的NFA可表示成如下的状态转换图:该图含有m个状态结点,每个节点可射出若干条箭弧与别的结点相连接,每条弧用Σ*中的一个字(不一定要不同的字而且可以使空串ε)做标记,整张图至少含有一个初态结点以及若干个(可以是0个)终态结点。某些结点既可以是初态结点也可以是终态结点。
例:已知NFA M=$({0,1,2,3},{a,b}, f , S_0,{3})$其中f为:
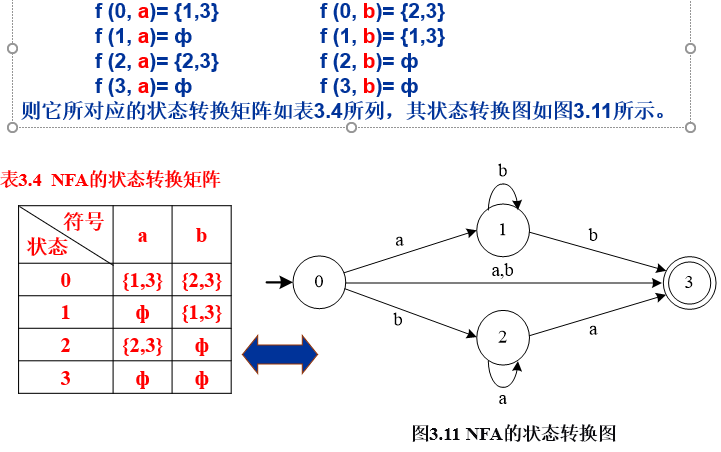
非确定有限自动机识别的语言
对于Σ*中的α,若存在一条从某一初态结点到某一终态结点的通路,且这条通路上所有箭弧的标记字依序连接成的字(忽略那些标记为ε的弧)等于α,则称α可为NFA M所识别(即接受)。
NFA M所能识别的所有字的集合称为该自动机识别的语言,记为L(M)。
若M的某些结点既是初态结点又是终态结点,或者存在一条从某个初态结点到某个终态结点的ε通路,那么,空字ε可为M所接受
如图所示的就是一个NFA,该NFA能识别Σ上所有含有相继两个a或相继两个b的字
DFA与NFA的关系
DFA 是NFA的特例,凡是能被DFA接受的符号串必然能被NFA所接受。NFA与DFA的区别在于DFA只有唯一的一个初态, NFA有一个非空初态集(即可以有若干初态);DFA的转换函数f是一个单值函数,NFA的转换函数f是一个多值函数。
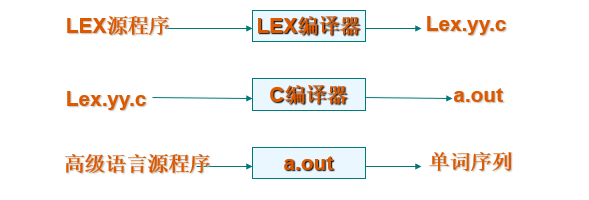
词法分析器的自动生成
Lex是一个基于正规式的描述构造词法分析器的工具,也称为Lex编译器,它已经广泛用于产生各种语言的词法分析器。它输入的是用Lex语言编写的源程序,输出的是词法分析的C语言程序。 Lex的流程如下图所示
LEX正则约定
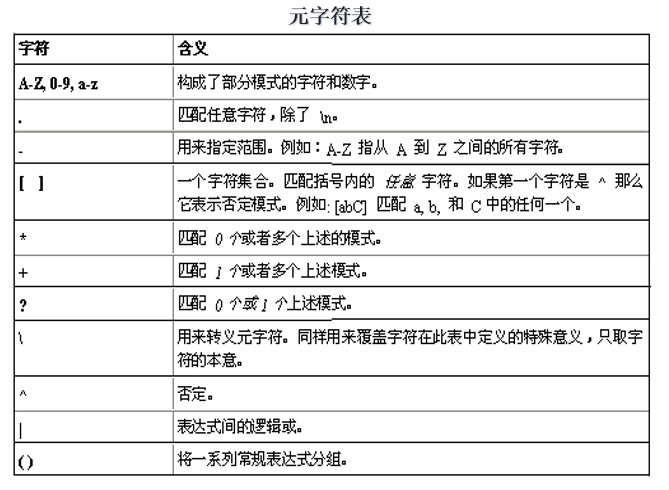
LEX的元字符约定
lex源程序的结构(lex输入文件的格式)
说明部分(辅助定义部分)
% %
识别规则部分
% %
辅助程序部分(用户子程序部分)
其中规则部分是必须的,定义和辅助程序部分是任选的。如果没有辅助程序部分,则第二个分隔号%%(双百分号)可以省去;但由于第一个%%用来指示规则部分的开始,故即使没有说明部分,也不能将其省去
说明部分
它是 C 和 Lex 的全局声明。它的作用,在于对规则部分要引用的文件和变量进行说明,通常可包含头文件,常数定义、全局变量定义、正则式定义等。每一个正则式定义由分隔符(适当个数的空格或制表符)连接的正则式的名字和正则式表达式组成,即: $D_i R_i$
其中,$ D_i$表示正则式的名字,Ri表示正则表达式。除正则式定义以外,定义部分的其余代码须用符号%{和%}括起来,其间可以是包括include语句、声明语句在内的C语句。
%{
int wordCount = 0;
int noCount = 0;
%}
chars [A-za-z]
numbers ([0-9])+
words {chars}+
注意
凡是对已经定义的正则表达式的名字的引用,都必须用花括号将它们括起来。在LEX源程序中,起标识作用的符号%%,%{以及%}都必须处在所在行的最左字符位置。
识别规则部分
识别规则部分起始于“%%”符号,终止于“%%”符号,其间则是词法规则。词法规则由词形和动作两部分组成。即: $ P_i$ {ACTION i} $P_i$词形部分可以由任意的正则表达式组成,ACTION i动作部分是由C语言语句组成,这些语句用来对所匹配的词形进行相应处理。规则部分完全决定了词法分析程序的功能,它只能识别出词形中正则表达式所定义的单词。
例如:
%%
{words} {wordCount++; /*increase the word count */ }
{numbers} {noCount++; /*increase the number count */ }
\n {;}
. {;}
辅助程序部分
这部分包含了识别规则部分的动作代码段中所调用的各个局部函数,着写函数由用户用C语言编写的,这样就可以达到简化编程的目的。它们将由LEX系统直接拷贝到输出文件lex.yy.c中。
例如:
%%
main( )
{
yylex(); /* start the analysis*/
printf(" Count of words:%d\n", wordCount);
printf(" Count of nombers:%d\n", noCount);
}
综合上述几个例子,我们可以编一个字(由字母组成的)和数字(由数字组成)的个数统计的词法分析器了。
LEX输入源程序
%{
int wordCount = 0 ,noCount=0;
%}
chars [A-za-z]
numbers ([0-9])+
words {chars}+
%%
{words} {wordCount++; /*increase the word count */ }
{numbers} {noCount++; /*increase the number count */ }
\n {; /*do nothing */ }
. {; /*do nothing */ }
%%
main( )
{
yylex(); /* start the analysis*/
printf(" No of words:%d\n", wordCount);
printf(" Count of nombers:%d\n", noCount);
}
非确定有限自动机的确定化
补充算法
已知NFA $M_N$=(S,Σ,f,$S_0$,Z),假设与之等价的DFA $M_D$ =(S’,Σ,f’,$S_0’$,Z’),其中:
- DFA $M_D$ 的状态集S’就是S的一切子集组成的集合;
- Σ不变;
- $S_0’= S_0$ ;
- S’中含有NFA $M_N$的终态子集就是DFA $M_D$ 的终态的集合Z’;
- DFA MD转换函数f’的构成:若${p_1,p_2, …,p_k}$是DFA $M_D$的一个状态,则 $f’({p_1,p_2, …,p_k},a)= f(p_1,a) ∪f(p_2,a) ∪ … ∪ f(p_k,a)$
通过上述步骤,便可得到与NFA $M_N$等价的DFA $M_D$等价,从而得到与之对应的状态转换矩阵和状态转换图。
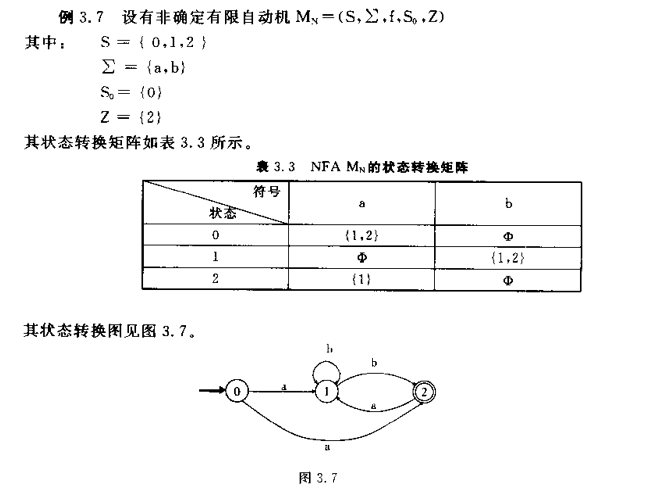
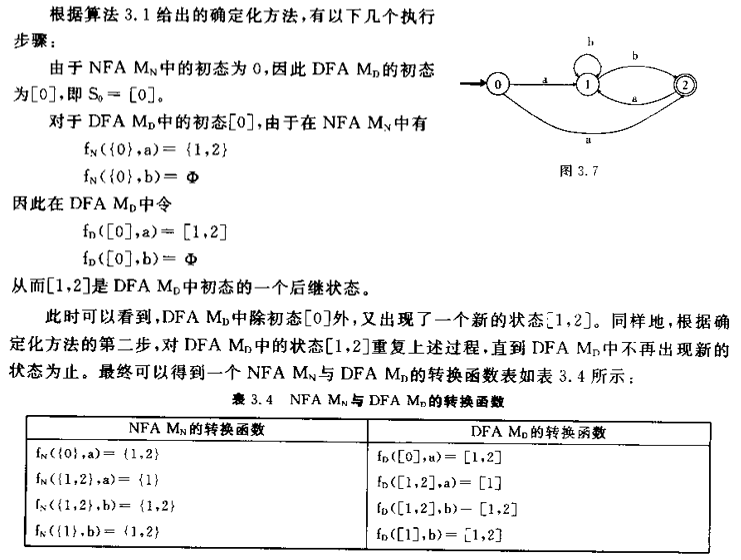
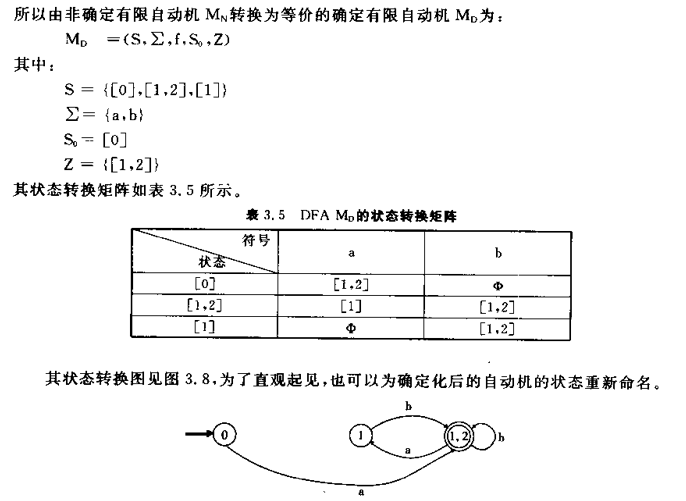

非确定的有限自动机和确定的有限自动机从功能上来说是等价的,它们所接受的语言类相同。给定任一不确定的有限自动机NFA M,就能构造一个确定的有限自动机DFA M",使得L(M)=L(M")
状态集I的ε闭包
假定I是一NFA M的状态集S的一个子集,则ε_closure(I) 称为状态集I的ε闭包,ε闭包也是状态集S的一个子集,其计算方法如下:
- 若q∈I,则q∈ε_closure(I),即I的所有成员都是I的ε闭包的成员;
- 若q∈I,那么从q出发经过任意条ε弧而能到达的任何状态都属于ε_closure (I)。
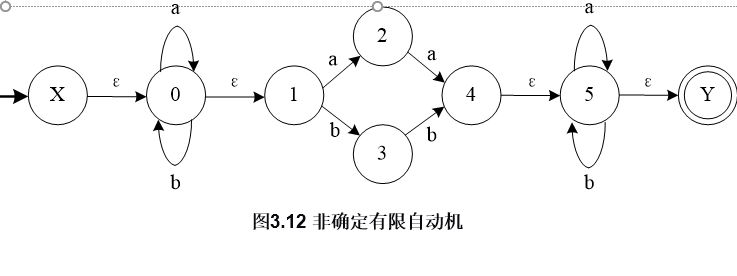
例:对图所示的NFA M,求I={1}、I={2}、I={1,2}的ε闭包。
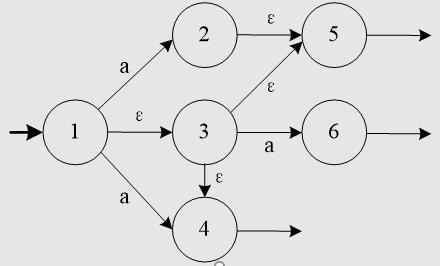
解: 当I={1}时,有f(1,ε)=3,f(3,ε) =5,f(3,ε) =4, 则有 ε_closure({1})={1,3,4,5}; 当I={2}, 有f(2,ε)=5, 则有ε_closure({2})={2,5} 当I={1,2}, 则有ε_closure({1,2})=ε_closure({1})∪ε_closure({2}) ={1,3,4,5}∪{2,5} ={1,2,3,4,5}
状态集I的a弧转换集
假定I是一NFA M的状态集S的一个子集,I={ $P_1, P_2,…,P_n$ }, a∈∑,即a是字母表∑ 的一个输入符号,则P的a弧转换集为:

即J是从状态子集I中的每个状态出发,沿着标记为a的箭弧而转移到达的状态所组成的集合。
从定义可知,状态集I的a弧转换集Ia也是状态子集,其元素为从I的每个状态出发,沿着标记为a的箭弧所转移到达的每个后继状态的ε闭包。
非确定有限自动机的确定化方法(子集法)
过程如下:
-
假定NFA M=(S, Σ, f,S0,Z),首先对NFA M的状态转换图进行改造:
- 引进新的初态结点X和终态结点Y(X S,Y S),从X到S0任意状态结点连一条ε箭弧,从Z中任意状态结点连一条ε箭弧到Y
- 对M的状态转换图进行图所示的替换,其中k是新引入的状态。重复这种分裂过程直至状态转换图中的每条箭弧上的标记或为ε,或为Σ中的单个字母。将最终得到的NFA Mˊ,显然L(Mˊ)=L(M)。

-
对改造后的NFA Mˊ使用子集法进行确定化
-
对Σ={a1,…,ak},构造一张表,该表的每一行含有k+1列。置该表的首行首列为ε_CLOSURE({X}),它就是DFA的唯一初态

-
如果某一行的第一列的状态子集已经确定,如记为I,那么,置该行的i+1列为Iai(i=1,….,k)。然后,检查该行上的所有状态子集,看它们是否已在表的第一列中出现,将未曾出现者填入到后面空行的第一列。重复上述过程,直至出现在第i+1列(i=1,…,k)上的所有状态子集均已在第一列上出现。
-
**将构造出来的表视为状态转换矩阵,将其中的每个状态子集视为新的状态,就得到了一个DFA M"。它的初态是该表首行首列的那个状态,终态是那些含有原来NFA M的任一终态的状态子集。 **
-
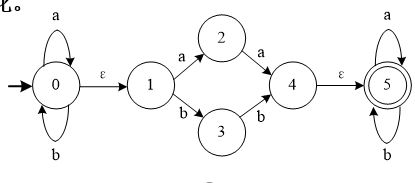
例:已知有非确定的有限自动机NFA M,具体如图所示,利用子集法将它确定化。
解:
-
改造状态转换图,引进新的初态结点X和终态结点Y,得到新的状态转换图如图所示。

-
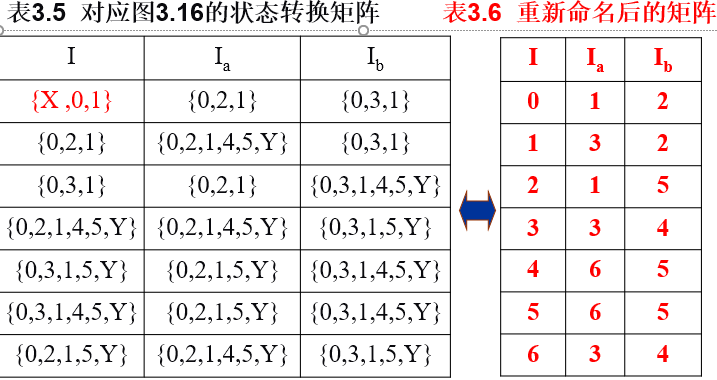
构造状态转换矩阵,因为f(X,ε)=0,f(0,ε) =1,所以ε_CLOSURE(X) ={X ,0,1},根据子集法可构造出所有状态子集,具体见表3.5。对表3.5中的所有状态子集重新命名,得到表3.6所列的状态转换矩阵。

-
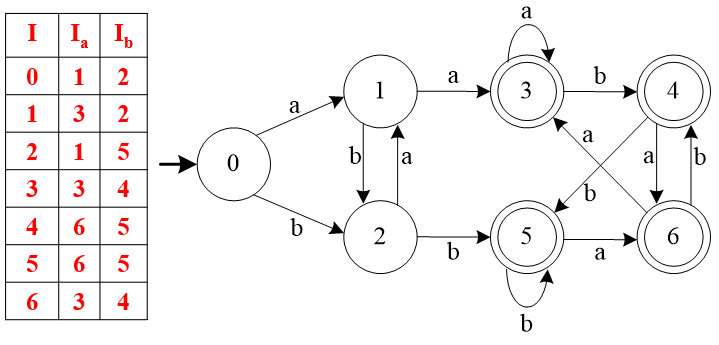
与表3.6相对应的状态转换图如图3.17所示,其中0为初态,3﹑4﹑5和6为终态。显然,图3.15和图3.17所示的有限自动机是等价的。

确定有限自动机的化简
确定有限自动机DFA M的化简是指:寻找一个状态数比M少的DFA Mˊ,使得L(M)=L(Mˊ)。化简的方法就是消除DFA M中的无关状态,合并等价状态。
通常把无用状态和死状态统称为无关状态。
所谓无用状态,就是指从初态出发,读入何输入串都不可能到达的状态;
所谓死状态,就是对于任何输入符号,该状态的后继状态都是它自身,而不可能从它到达终态。
如图所示的状态转换图中,状态1是无用状态,状态2是死状态,状态1、2均为无用状态
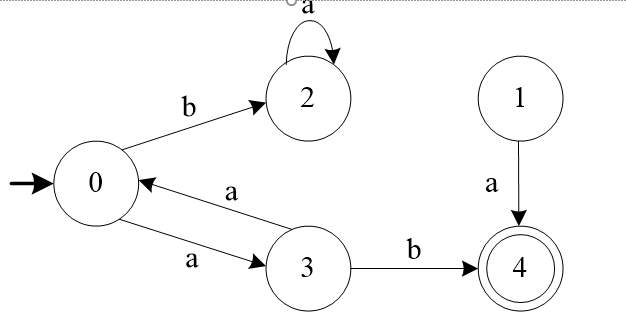
DFA M的状态最小化过程的核心思想:将DFA M的状态集分割成一些不相交的子集,使得任何不同的两子集中的状态都是可区别的,而同一子集中的任何两个状态都是等价的。最后,在每个字集中选出一个代表,同时消去其它等价状态。
具体过程如下:
-
把DFA M的所有状态集S分成两个子集——终态集与非终态集,形成基本分划∏。显然,属于这两个不同子集的状态是可区别的。
-
对各状态子集按下面的方法进一步划分
假定经过第i次划分后,∏={$S_1,S_2,….,S_m$},其中的任何一个都是状态子集。对于任意一个状态子集Sj={$q_1,q_2,….,q_k$},若存在一个输入字符a∈Σ,使得($S_j$)a(即将子集Sj的所有状态读入a所到达的状态的集合)不全包含在现行∏的某一子集中,就将$S_j$一分为二。
-
经上述过程之后,得到一个最后分划∏。对于∏中的每一个子集,选取子集中的一个状态代表其他状态,删除其他一切的等价状态。例如,假定∏中有子集$S_j={q_1,…,q_k}$,则可将$q_2,…,q_k$从原来的状态集中删除。若$S_j$中含有原来的初态,则$q_1$是新初态;若$S_j$中含有原来的终态,则$q_1$是新终态。
通过上述步骤进行化简后,再删除所有的无关状态,便可以得到最简的DFA M
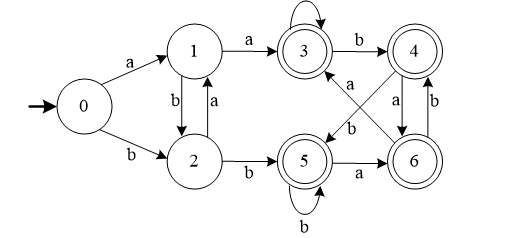
例:已知有图所示的DFA M,试写出其最小化过程。
解:
首先,把DFA M的状态分成两个子集:终态集{3,4,5,6},非终态集{0,1,2},即S={3,4,5,6}∪{0,1,2}。
其次,考察子集{3,4,5,6},由于{3,4,5,6}a={3,6} {3,4,5,6}和{3,4,5,6}b={4,5} {3,4,5,6},所以,它不能再分划。
再考察{0,1,2},由于{0,1,2}a={1,3},它既不包含在{3,4,5,6}之中也不包含在{0,1,2}之中,因此,应把{0,1,2}一分为二。由于状态1经a箭弧到达状态3,而状态0和2经a箭弧都能到达状态1,因此,应把1分出来,形成{1},{0,2}。
现在,整个状态集划分成三个子集,即S={3,4,5,6}∪{1}∪{0,2}。
由于{0,2}b={2,5}未包含在上述三个子集中的任何一个子集之中,故{0,2}也应一分为二:{0},{2}。
至此,整个划分结束,状态集分成四个子集,即S={3,4,5,6}∪{0}∪{1}∪{2},且每个子集都已不可再分。
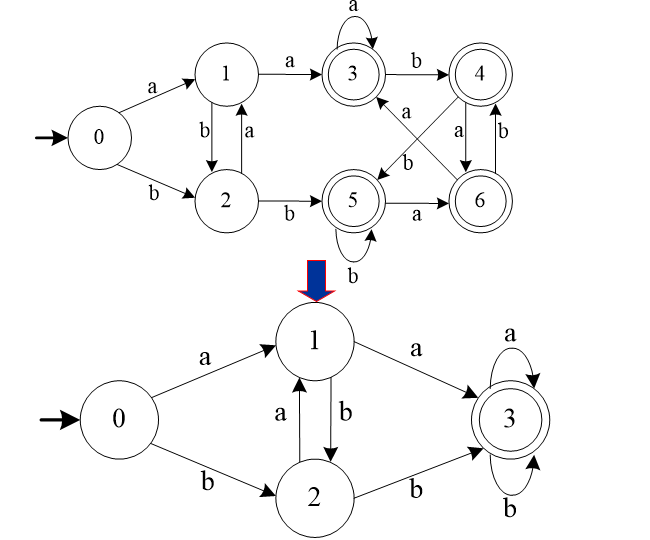
正规文法与有限自动机的等价性
一个正规集可以由正则文法产生,也可以用有限自动机来识别,对于正规文法G和有限自动机M,如果L(G)=L(M),则称G和M是等价的。对于正规文法和有限自动机的等价性,有以下两个结论:
- 对任一正规文法G($G_R$右线性文法和左线性文法$G_L$),都存在一个有限自动机(FA)M,使得$L(M)= L(G_R)=L(G_L)$。
- 对任一有限自动机FAM,都存在一个正规文法($G_R$右线性文法和左线性文法$G_L$),使得$L(M)=L(G_R)=L(G_L)$。
右线性文法→有限自动机
设右线性文法$G_R=(V_T,V_N, P,S)$,$NFA为(S,Σ, f,S_0,Z)$。根据右线性文法的四个部分求NFA的五个部分。
-
文法$G_R$的开始符号S就是NFA的初态;
-
文法$G_R$的$V_T$就是NFA的输入字母表Σ;
-
为NFA引入一个终态符号Z’,$Z \notin V_N$,则NFA的终态集Z={Z’};
-
文法GR的$V_N∪{Z’}$构成NFA的状态集S;
-
利用文法$G_R$的产生式集P来构成NFA的转换函数f,具体方法如下:
若对于某个$A∈V_N$及$a∈V_T∪{ε}$,P中产生式A→a,则令 f(A,a)=Z’。
对任意的$A∈V_N及a∈V_T∪{ε}$,设P中左端为A,右端第一符号为a的所有产生式为:$A→aA_1|….|aA_k$(不包括A→a),则令 $f(A,a)={A_1,…,A_k}$。
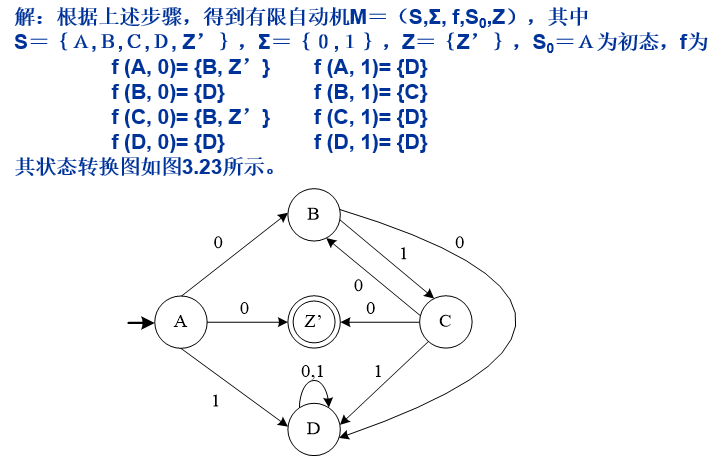
例:已知$G_R[A]=({A,B,C,D},{0,1},A,P)$,其中产生式集P为:

有限自动机→右线性文法
-
有限自动机转换成右线性文法,需要满足一个条件:有限自动机只有一个初态结,且终态结没有非 $ \varepsilon $ _弧射入。 如果不满足,则须进行改造。具体工作如下:
- 如果M有多个初态结,则引入一个新的初态结,并从新的初态结引一_弧到原初态结,原初态结则不再作初态。
- 如果M的终态结有射入弧,则引入一新的终态,并从原来的任意终态结引一$\varepsilon$_弧到新终态结,原终态结则不再作终态
-
构造过程:
有限自动机M的输入字母表Σ就是文法G的终结符号集$V_T$; 初态结就是文法G的开始符号S;文法G的产生式集P由M的转换函数f得到:
若f(A,a)=B,则A→aB 若f(A,a)=Z’,其中Z’∈Z,则A→aM的终态不会出现在文法的产生式中,所以$V_N$为M的状态集S去掉终态集Z中的状态构成,即$V_N=S-Z$。
例:
将下图有限自动机转换成右线性文法:
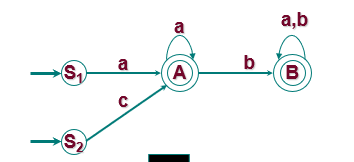
右线性文法$G[S]=(V_N,V_T,P,S)$,其中$V_N ={S,S_1,S_2,A,B}$ , $V_T ={a,b,c}$,P由下列规则组成:
$S →S_1∣S_2$
$S_1→aA$
$S_2→cA$
$A →aA∣ bB ∣ \varepsilon$
$B →bB∣ aB ∣ \varepsilon $
左线性文法→有限性自动机
设左线性文法$GL=(V_T,V_N,P,S)$,$NFA为(S,Σ, f,S_0,Z)$。根据右线性文法的四个部分求NFA的五个部分。
- 文法$G_L$的开始符号S就是NFA的终态;
- 文法$G_L$的$V_T$就是NFA的输入字母表Σ;
- 为NFA引入一个初态S’,$S’ \notin VN$,则NFA的初态集$S_0 ={S’}$;
- 文法$G_L$的$V_N∪{S’}$构成M的状态集S;
- 利用文法$G_L$的产生式集P来构成NFA的转换函数f,具体方法如下:
- 若对某个$A∈V_N及a ∈V_T∪{ε}$,P中有产生式A→a,则令 f(S’,a)=A。
- 对任意的$A∈V_N$及$a ∈V_T∪{ε}$,若P中所有右端第一符号为A,第二个符号为a的产生式为:$A_1→A_a|,….,A_k→Aa$,则令 $f(A,a)={A_1,….,A_k}$。
例:
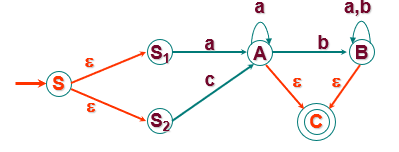
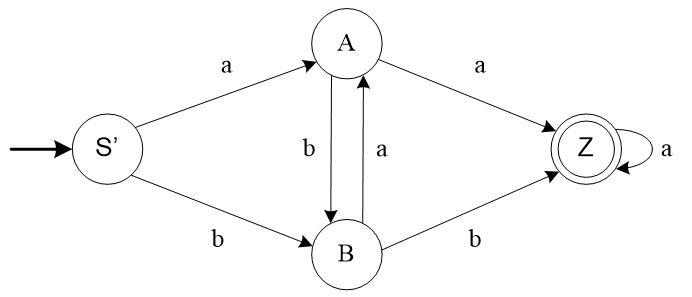
已知有左线性文法G[S]:
S→Sa | Aa|Bb
A→Ba | a
B→Ab| b
试构造与文法G[S]等价的有限自动机。
解:按照左线性文法到有限自动机的转换方法,为有限自动机引入一个初态S’;因为文法G[S]的开始符号S作为有限自动机的终态(设该终态为Z’),为了方便设计,避免混淆现将所有产生式中的S替换成Z。
有限自动机→左线性文法
有限自动机转换成左线性文法,需要满足一个条件:有限自动机只有一个终态结,且初态结没有非$\varepsilon _$弧射入
如果它不满足,则须对进行改造,具体工作如下:如果NFA M有多个终态结,则引入一个新的终态结,并从原来的终态结各引_弧到新的终态结(原终态结则不再作终态)。如果NFA M的初态结有射入弧,则引入一新的初态,并从该初态结各引一_弧到原初态结(原初态结则不再作初态)
一般的,改造后的非确定有限自动机$NFA M=(S,Σ, f,S_0,Z)$,由它构造左线性文法$G_L=( V_N,V_T, P, S)$的方法是:
- NFA M的输入字母表Σ就是文法$G_L$的终结符号集$V_T$;
- NFA M的唯一终态结就是文法$G_L$的开始符号;
- 文法$G_L$的产生式集P由NFA M的转换函数f得到,具体方法是:
- 若f(A,a)=B,则B→Aa∈P;
- 若f(S’,a)=B,其中S’∈$S_0$,则B→a∈P;
- 显然,NFA M的初态不会出现在文法的产生式中,所以$V_N$为NFA M的状态集S去掉初态集$S_0$中的状态构成,即$V_N=S-S_0$。
例:
将上图的有限自动机转换成与之等价的左线性文法
解:按照有限自动机到左线性文法的转换方法,由于该有限自动机有多个终态,则引入一新终Z,则改造后的有限自动机如图所示
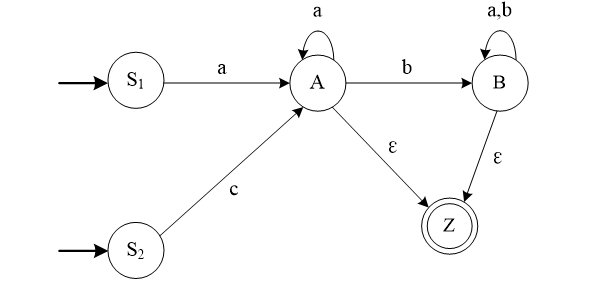
按上述方法,与该自动机相应的左线性文法为$G[Z]=( V_N, V_T,P,Z)$,其中,Z 是文法开始符号,$V_N ={Z,A,B}, V_T ={a,b,c}$,P的规则如下:
**Z→A | B **
A→Aa | a | c
**B→Ba |Bb| Ab **
正则表达式与有限自动机的等价性
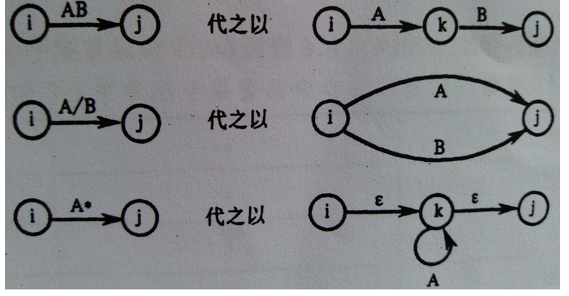
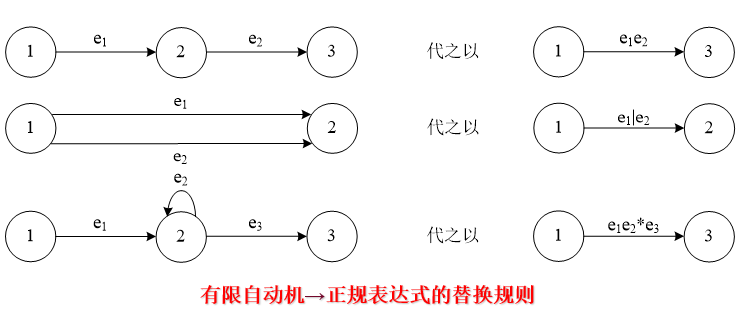
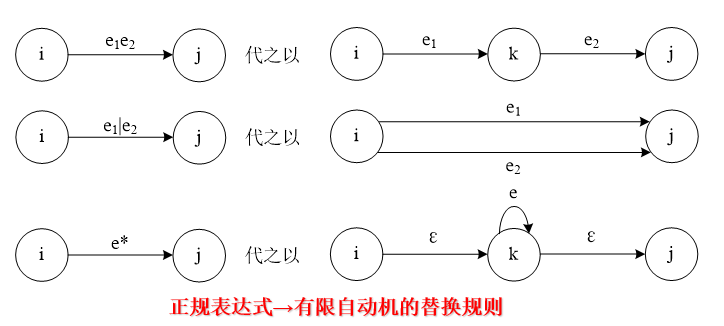
- 有限自动机→正则表达式,具体步骤如下:
- 首先拓广转换图的概念,允许每条箭弧用正则表达式作标记。
- 在FA M的转换图上加进一个初态结X和一个终态结Y,从初态结X用弧连接到M的所有初态结;从M的所有终态结用弧连接到Y结;
- 反复用替换规则,对自动机进行消弧,直到只剩下一个初态X,一个终态Y,和一条箭弧为止,则箭弧上的标记的正则表达式就是所求的e。
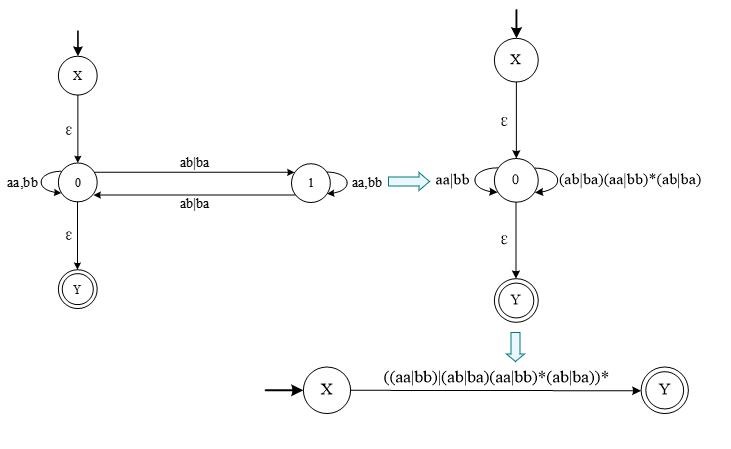
例:
已知有一个非确定的有限自动机NFA M如图3.29所示,试转换出与之等价的正规式

解:按照有限自动机到正规式的转换方法,首先引入一个初态X和一个终态Y,得到如图所示的状态转换图。
正则表达式e→有限自动机FA M
具体步骤如下:
- 先构造一个FA M的一个广义转换图,其中,只有X与Y两个状态,X是初态,Y是终态,弧上是正规表达式e。
- 然后,按照替换规则对正规表达式e逐步进行分解,直到转换图中所有的弧上都是中的单个符号或$\varepsilon$为止。
例:
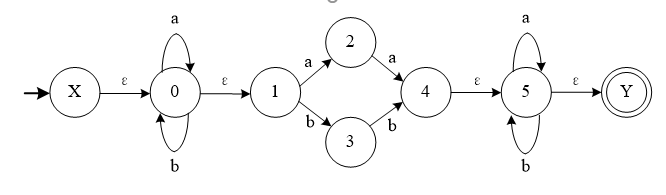
构造与正规式$ (a|b)^(aa|bb)(a|b)^$ 等价的非确定的有限自动机
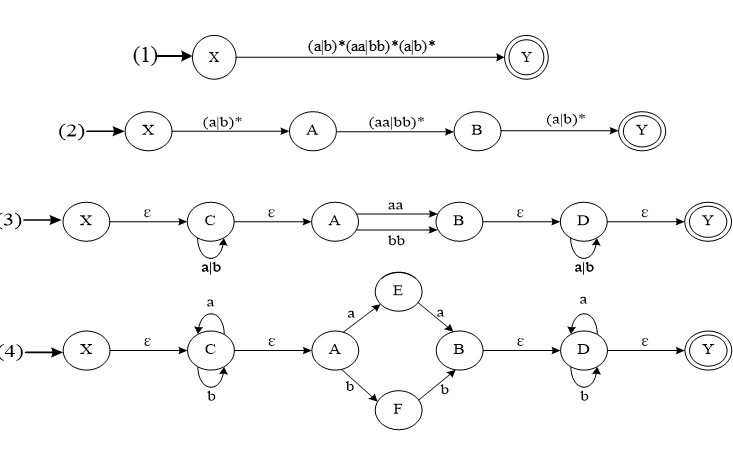
注:第1,2步骤中的$ (a|b)^(aa|bb)^(a|b)^$和$(aa|bb)^$要改为$ (a|b)^(aa|bb)(a|b)^$和$(aa|bb)$