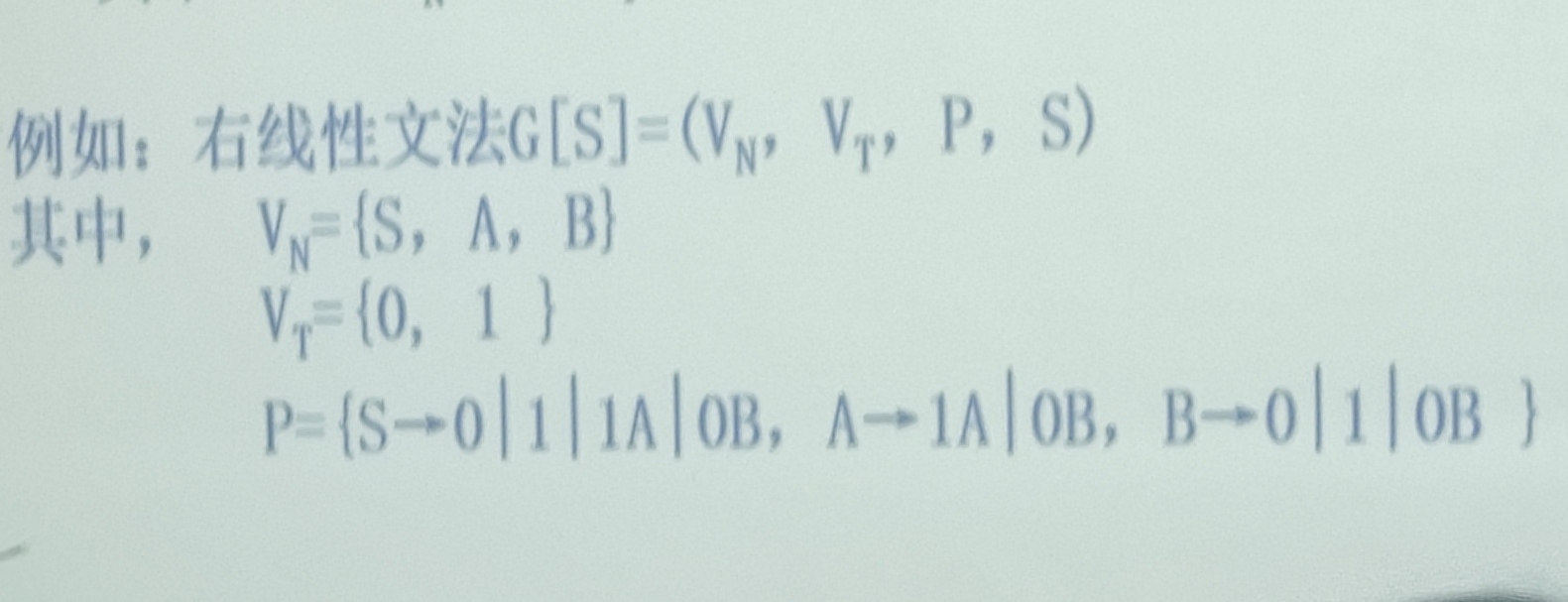高级语言的定义

语法

任何高级语言程序都可以看成是一个特定字母表(即元素的非空有穷集合)上的一个字符串(有穷序列)

词法规则

指单词符号的形成规则，它确定语言的单词符号，单词符号一般包括：标识符，保留字，界符，算符等

语法规则

从单词符号形成更大的结构(即语法单位)，它是语法单位的形成规则，一般语法单位有：表达式，语句，函数，程序等

语义

定义它的单词符号和语法单位的意义
所谓一个语言的语义是指这样的一组规则，使用它可以定义一个程序的意义

文法和语言

基本概念

字母表

1. 字母表：元素的非空有穷集合，习惯上用大写字母表示，如 ∑ ={a,b}
2. 符号:字母表中的每一个元素，如a,b;

符号串

1. 符号串:字母表中的符号的有穷序列，如 a,b,aa,bb….。
2. 空符号串：不含任何符号的符号串，记为ε
3. 符号串集合：字母表∑上的符号串组成的集合。

符号串运算

1. 符号串长度：符号串中所包含的符号个数。设符号串为x,则其长度记为|x|。

2. 符号串连接:设有符号串x和y，把y的所有符号相继写在x的符号串之后所得到的符号串即称为x和y的连接，记为xy

   例：εx=xε=x

3. 符号串的方幂：设x的符号串，则x的n次连接称为n次方幂，记为xn。

   例：$x^0$=ε

4. 符号串的前缀，后缀，子串

   假设x是一个符号串，则有：

   符号串x的前缀是指：从符号串x的尾部删除若干(含0个)符号后得到的符号串；

   符号串x的后缀是指：从符号串x的头部删除若干(含0个)符号后得到的符号串：

   符号串x的子串是指：删除了x前缀(或删除x的后缀或删除x的前缀和后缀)后得到的符号串；

   对任意的符号串x，x的前缀，后缀都是x的子串，但x的子串不一定是x的前缀或后缀。

   对任意的符号串x，x和ε都是符号串x的前缀，后缀，也是x的子串。

符号串集合的运算

1. 符号串的集合的乘积

   设A，B为符号串集合，则符号串集合的乘积表示为AB={xy|x∈A,y∈B},即A中的任意符号串和B中的任意符号串的连接所构成的集合。

   以为有 xε=εx=x,所以有{ε}A={ε}A=A

   注：∅A= A∅ =∅

2. 符号串集合的方幂：即同一个符号串集合的乘积。

   例：设A为符号串集合，则

   $A^0$={ε} , $A^1$=A, $A^2$=AA,…..

符号串集合的闭包

星闭包

设A为符号串集合，则$A^*$为符号串集合A的星闭包。具体定义如下：

$A^*=A^0\bigcup$$A^1$$\bigcup$$A^2$$\bigcup$$A^3$$\bigcup$…..

正闭包

设A为符号串集合，则$A^+$为符号串集合A的正闭包。具体定义如下：

$A^+=A^0\bigcup$$A^1$$\bigcup$$A^2$$\bigcup$$A^3$$\bigcup$…..

**由上述两个定义，显然有 :$A^+$ $=$ $AA^*$ **

文法及文法的BNF表示

规则

即产生式，是一有序对(U，ⅹ)，通常记为： U→x(或U::x)

文法和字汇表

文法可以定义成一个四元组G=($V_N$,$V_T$,S,P)

1. $V_N$:一个非空有限的非终结符号集合
2. $V_T$:一个非空有限的终结符号集合
3. S:文法的开始符号，它是一个特殊的非终结符号
4. P:产生式的有限集合

例如：

文法的BNF(巴科斯范式)表示

为了书写简洁，常常把左部相同的规则缩写在一起，使其结构更加紧凑，在规则中引入符号"|",以表示“或者”。形如$S\rightarrow$$a_1$,$S\rightarrow$$a_2$,….,$S\rightarrow$$a_n$,缩写为$S\rightarrow$$a_1$|$a_2$|….|$a_n$,每个$a_i$被称为S的一个候选式

因此，上述例子的文法还可以写成：

递归规则及递归文法

递归规则

指那些在规则的右部含有与规则左部相同符号的规则，例如，$U\rightarrow$$xUy$,右部含有与规则左部相同部分符号U，这就是递归规则

如果这个相同符号出现在右部的最左端，则为左递归规则，例如:$U\rightarrow$$Uy$

如果这个相同符号出现在左部的最右端，则为右递归规则，例如:$U\rightarrow$$xU$

递归文法

若文法中至少包含一条递归规则，则称文法是直接递归的

例如：

算术表达式G[E]:

$E\rightarrow$$E+T|T$

$T\rightarrow$$T*F|F$

$F\rightarrow$$(E)|i$

显然，该文法就是一个直接递归文法

推导和归约

直接推导

设$\alpha\rightarrow$$\beta$是文法$G=(V_N,V_T,S,P)$的产生式，$\gamma$和$\delta \in (V_N \bigcup V_T)^*$,若有符号串v,w满足：

$v=\gamma\alpha\delta$，$w=\gamma\beta\delta$

则称v(利用规则$\alpha\rightarrow\beta$)直接推出w，或则说w是v的直接推导，记作:$v\Rightarrow w$.

归约是推导的逆过程，若$v\Rightarrow w$,也可以说w直接规约到v

长度为n的推导

如果存在直接推导的序列:$v=w_0\Rightarrow w_1\Rightarrow …. \Rightarrow w_n = w (n\geq1)$，则说v经过n步(n>0)推导出w，记作：$v\stackrel{+}\Rightarrow w$。“$\stackrel{+}\Rightarrow$”表示多步直接推导。

若有$v\stackrel{+}\Rightarrow w$,或v=w(n=0),则说v经过n($n\geq 0$)步推导出w，记作：$v\stackrel{}\Rightarrow w$。“$\stackrel{}\Rightarrow$”表示0步或多步直接推导。

最左推导和最右推导

若在推导过程中，每一步总是对当前符号串最左(右)边的非终结符号进行替换，称为最左(右)推导。如果文法G是无二义的，那么最右推导的逆过程为最左归约，最有推导为规范推导，最左规约为规范归约。

句型，句子和语言

句型，句子

定义

设G[S]是文字表V上的一个文法，如果符号串u是由文法的开始符号推导出来的，则称u是文法G[S]的句型。如果u仅由终结符号组成，则称u是文法G[S]的句子

即：

若$S\stackrel{}\Rightarrow u$，$u\in V^$，则称u是文法G[S]的句型；

若$S\stackrel{+}\Rightarrow u$，$u \in V_T^*$，则称u是文法G[S]的句子；

语言

定义

文法G[S]所产生的所有句子的集合，称为该文法所定义的语言，记为L(G[S])。

即：

L(G)={u|$S\stackrel{+}\Rightarrow u$，且$u\in V_T^*$}

文法和语言的关系

1. 对于一给定的文法，可以唯一地确定它所产生的语言
2. 对于一给定的语言，可以找到若干不同的文法定义它

短语，简单短语，句柄

定义

设G是一个文法，S是文法G的开始符号，$\alpha\beta\delta$是该文法的一个句型，如果有：

$S\stackrel{*}\Rightarrow \alpha A \delta$并且 $A\stackrel{+}\Rightarrow\beta$

则称$\beta$ 是句型$\alpha\beta\delta$相对于非终结符号A的短语。特别的，如果$A\stackrel{+}\Rightarrow\beta$ 是通过1步推导来完成的，则称$\beta$是句型$\alpha\beta\delta$相对于非终结符号A的简单短语，也称为直接短语。一个句型的最左边的简单短语称为句柄

语法树与文法的二义性

语法树

用一张图来表示一个句型的推导过程

设文法G=($V_N,V_T,P,S$)，对于文法G的任意一个句型都存在一个相应的语法树：

1. 树中每个结点都有一个标记，该标记是$V_NV_T$中的一个符号；
2. 树的根节点标记文法的识别符号S；
3. 若树的一个结点至少有一个叶子结点，则该结点的标记一定是一个非终结符；
4. 若树的一个结点有多个结点，该结点的标记为A，这些叶子结点的标记从左到右分别是$B_1,B_2,…,B_n$，则($A\rightarrow B_1B_2…B_n$)$\in P$

二义性

定义

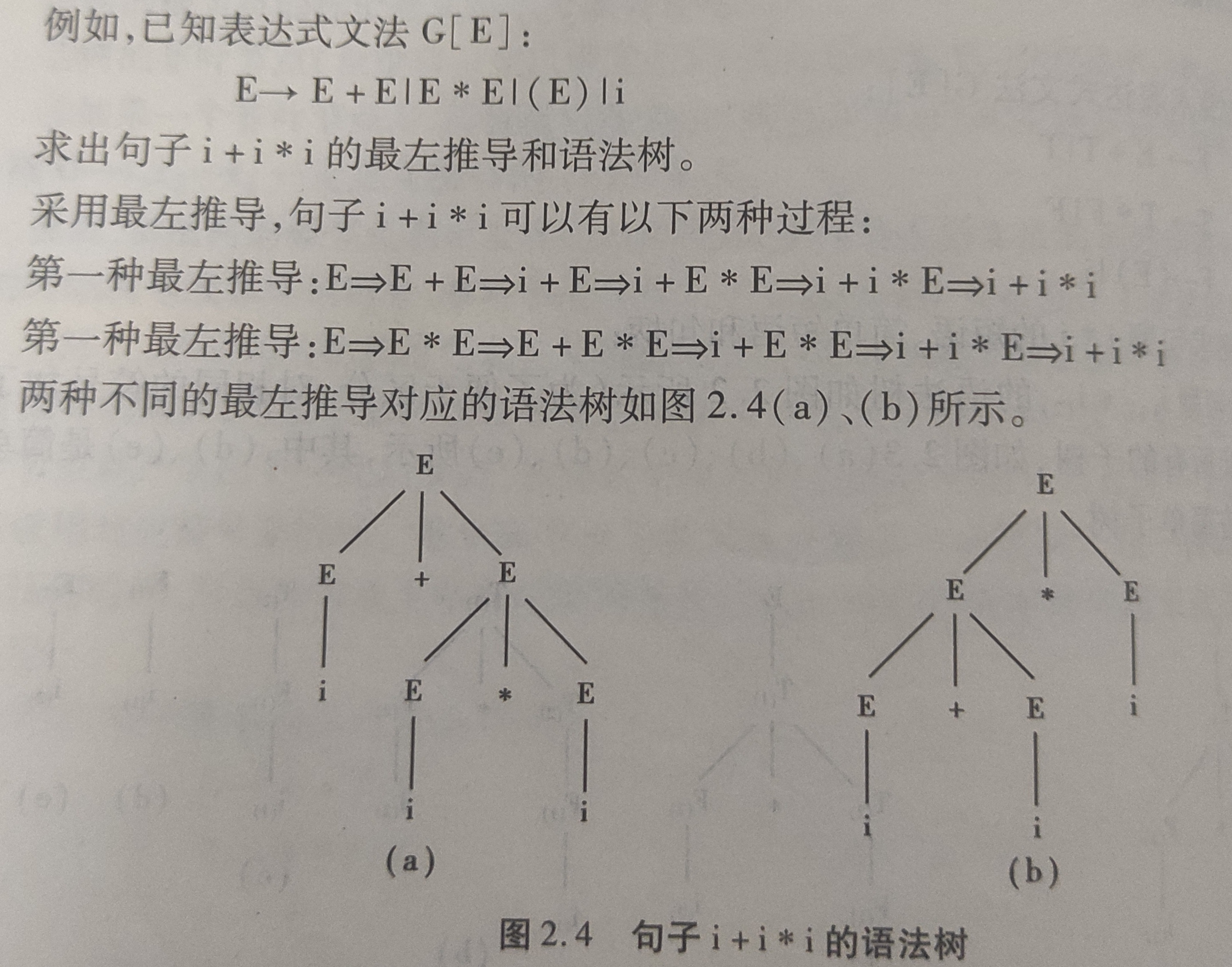
一个文法，如果它的一个句子由两颗或两颗以上的语法树，则称此句子具有二义性。如果一个文法含有二义性的句子，则该文法具有二义性。

注意

文法的二义性和语言的二义性是两个不同的概念。如果产生上下文无关语言的每一个文法都是二义性的，则说该语言是二义性的。并非文法的二义性就说其描述的语言是二义性的。通常可能有两个不同的文法G1和G2，其中一个文法是二义性的，另外一个是没有二义性的，但是却有L(G1) = L(G2)，即两个文法产生的语言是等价的

文法的实用限制

有害规则

定义：

文法中形如$U \rightarrow U$的规则就称为有害规则

如果文法中含有有害规则，它除了造成文法的二义性以外，对定义语言则是没有任何意义。

例如：

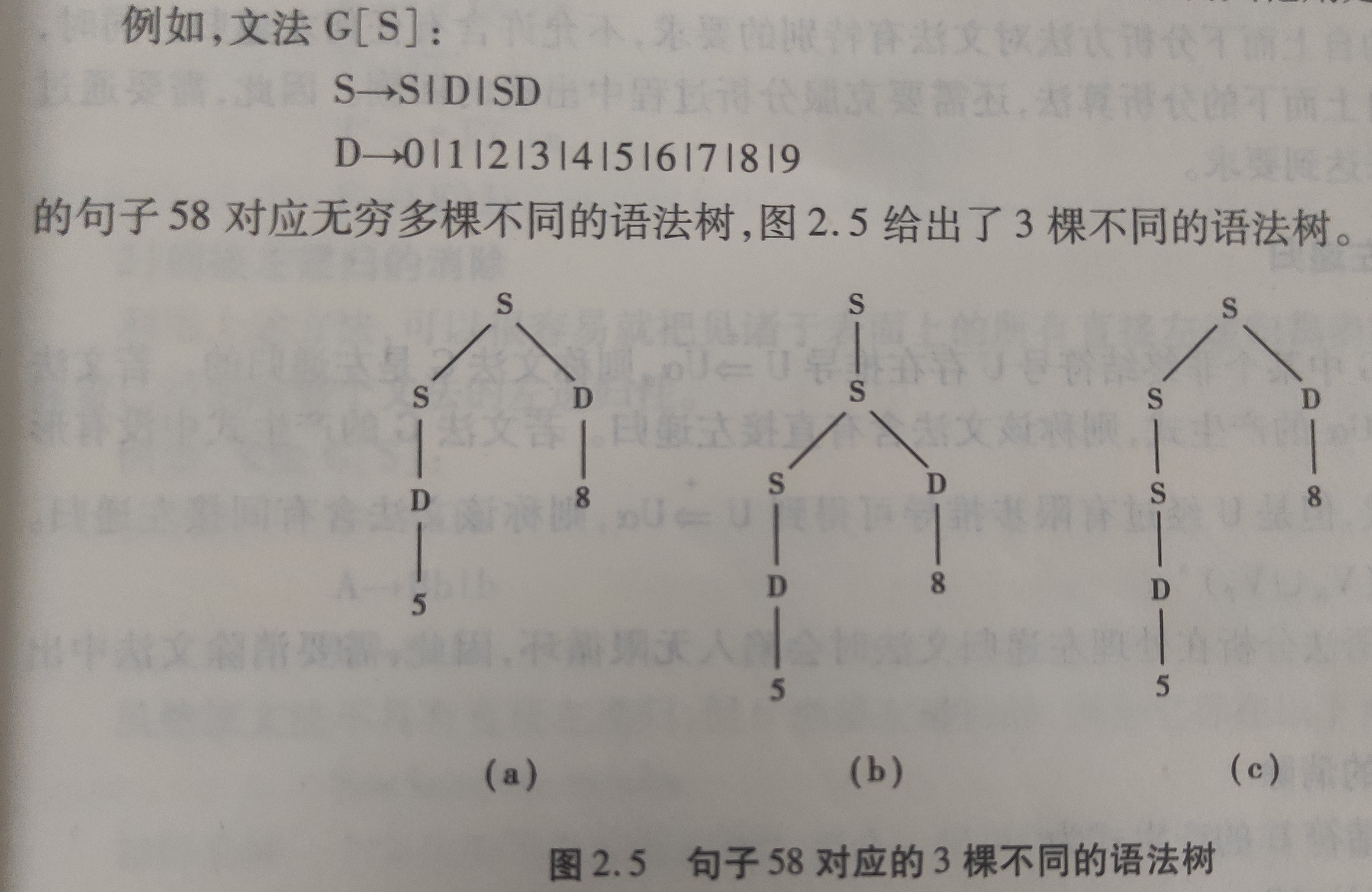
多余规则

多余规则则指文法中任何句子的推导都不会用到的规则，多余规则在文法中以两种形式出现，即不可到达的非终结符和不可终止的非终止符

1. 文法中某些非终结符(除去文法开始符号)不出现任何其他规则的右部，该非终结符称为不可到达。
2. 文法中某些非终结符，由它不能推出终结符号串，该非终结符称为不可终止。

例如：

G[S]:

1. $S\rightarrow Be$
2. $B\rightarrow Ce$
3. $B\rightarrow Af$
4. $A\rightarrow Ae$
5. $A\rightarrow e$
6. $C\rightarrow Cf$
7. $D\rightarrow f$

根据有害规则和多余规则的定义，显然文法不包含有有害规则，而由于非终结符号C为不可终止，非终结符号D为不可到达，因此产生式2，6，7为多余规则应去掉

一般所讨论的文法均假定不包含有有害规则和多余规则

文法的等价变换

文法直接左递归的消除

假定关于非终结符U的产生式为：$U\rightarrow U\alpha|\beta$

其中$\alpha ,\beta \in (V_N\bigcup V_T)^*$，$\beta$补以U开头，那么，可以把U的产生式改写成如下的非直接左递归形式：

$U\rightarrow \beta U^,$

$U^, \rightarrow \alpha U^,|\epsilon$

引入新的非终结符号消去文法中的直接左递归:

形如$U \rightarrow Ux_1 | Ux_2 |…| Ux_m|y_1|y_2|…|y_m$的规则，可引入一个新的非终结符号$U^,$,则得到等价的规则：

$U \rightarrow y_1U^,|y_2U^,|…|y_mU^,$

$U^, \rightarrow x_1U^,|x_2U^,|…|x_mU^,|\epsilon$

文法一般左递归的消除

如果一个文法不含有形如$U \stackrel{+}\Rightarrow U$的推导，也不含有以$\epsilon$为右部的产生式，那执行下面的算法将保证消除文法中的所有左递归

消除间接左递归的算法如下

例：

提取左因子

假设A的产生式为：

$A \rightarrow \delta\beta_1|\delta\beta_2|…|\delta\beta_n|\gamma_1|\gamma_2|…|\gamma_n$（其中，每个$\gamma$不以$\delta$开头）

可将这些产生式改写成：

$A \rightarrow A^,|\gamma_1|\gamma_2|…|\gamma_n$

$A^,\rightarrow \beta_1|\beta_2|…|\beta_n$

经过反复提取左因子，就能够把每个非终结符(包括新引进者)的所有候选式的公共左因子消除掉，则改变后的文法便于自上而下的语法分析，如LL(1)预测分析法。相应付出的代价是，大量引进新的非终结符和$\epsilon -$产生式。

例：

文法

0型文法

0型文法(无限制的文法)，其产生式具有以下形式：

$\alpha \rightarrow \beta$

其中，$\alpha \in V^+$，且至少含有一个非终结符；$\beta \in V^*$

1型文法(上下文有关文法)

定义：1型文法G的产生式具有以下形式：

$xUy \rightarrow \xuy$

其中$x,y \in V^*;U \in V_N;u \in V^+$

2型文法(上下文无关文法)

定义：在1型文法的产生式中上下文x和y用空符号串$\epsilon$代替，则有以下形式的产生式称为2型文法：

$U \rightarrow u$

其中，$U \in V_N,u \in V^*$

3型文法(正规文法)

定义1：如果文法的产生式只含有下面的两种形式：

$U \rightarrow a$或$U \rightarrow aB$

其中U，$B \in V_N,a \in V_T^*$，则称该文法为右线性文法；

定义2：如果文法的产生式只含有下面的两种形式：

$U \rightarrow a$或$U \rightarrow Ba$

其中U，$B \in V_N,a \in V_T^*$，则称该文法为左线性文法；

例：