概率算法

随机数

随机数在概率算法设计中十分重要。

计算机上无法产生真正的随机数。是一定程度上随机的, 是伪随机数线性同余法是产生伪随机数的最常用方法。

随机序列$a_0 ,a_1 ,…,a_n$满足：

$a_0=d$

$a_n=(ba_{n-1}+c)mod m$ n=1,2,..

其中$b \geq 0，c \geq 0，d\leq m$。d称为该随机序列的种子。

一般取m为机器大数，要求 gcd(m,b)=1，因此可取b为一素数

数值随机化算法

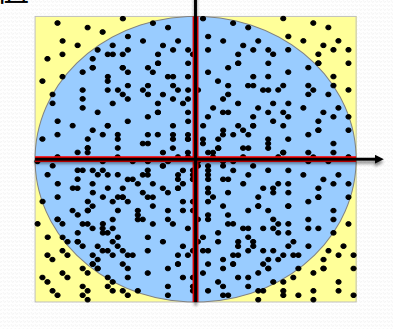
用随机投点法计算π值

设计一个半径r为1的圆外接正方 形，在该正方形内产生n随机点， 统计落在圆内的随机点的个数k，

则有 ： $ \frac{r^2}{4r^2} ≈ \frac {k}{n}$，

从而有：$𝜋 ≈ \frac{4k}{n}$

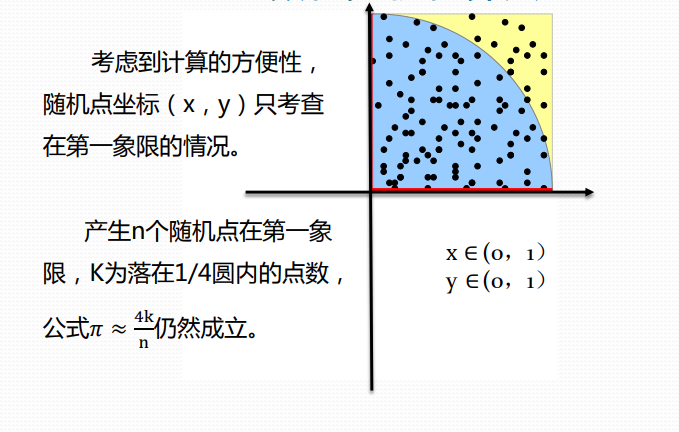
用随机投点法计算𝜋值算法

double Darts(int n)
{static RandomNumber dart;
	int k=0;
	for (int i=1;i <=n;i++) {
		double x=dart.fRandom();
		double y=dart.fRandom();
	if ((x*x+y*y)<=1) k++;
	}
	return 4*k/double(n);
}

计算定积分

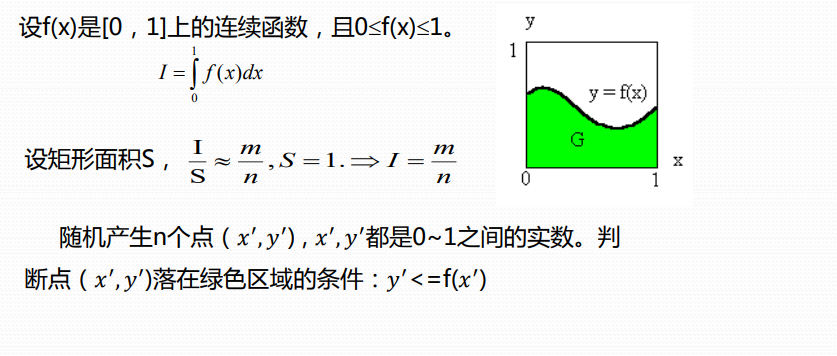
解非线性方程组

求解下面的非线性方程组

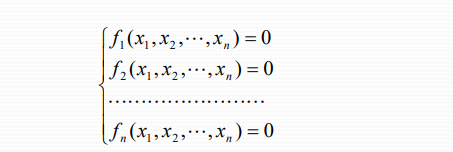
其中，x1 ,x2 ,…,xn是实变量，fi是未知量x1 ,x2 ,…,xn的非线性实函数。要求 确定上述方程组在指定求根范围内的一组解 $x^_1,x^_2,…,x^*_n$

1. 首先将多目标优化转为单目标优化：$F(X)=f1^2 (X) +f2^2 (X) …+fn^2 (X)=0$
2. 此问题只能找近似解，可设定误差$\varepsilon$
3. 在指定求根区域D内，随机搜素到一个点X, 当$F(X)< \varepsilon$时，即为所求 的近似解。否则继续搜索

以二维为例说明该算法

随机产生方向向量r，依可变步长a*r得到增量∆X，根据增量值∆X ，从 当前点移动到下一个点， 每到达一个新位置， 检查是否找到近似解

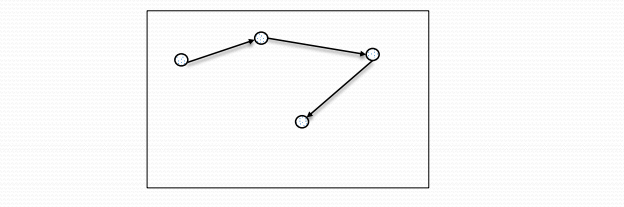
该类题目建议使用粒子群算法，或者模拟退火算法， 这两种方法求解 该类问题是更有效的，也是数值随机化方法

舍伍德(Sherwood)算法

概率算法-sherwood算法

拉斯维加斯( Las Vegas )算法

概率算法-Las Vegas

蒙特卡罗(Monte Carlo)算法

蒙特卡洛算法_monte carlo)算法

小结

1. 本章介绍利用随机数的随机性来解决问题。
2. 这些算法大多是非确定性算法。在某一时刻，下一步动作有多种选择。
3. 这些算法没有具体框架，分类是基于其算法的思想。
   1. 舍伍德算法：将算法加入概率算法，使算法不再有：对某些实例，算法的复杂 性必然很高的规律。
   2. 拉斯维加斯算法：引入随机化策略，运行一次算法可能找不到答案， 但运行多 次一定能找到答案
   3. 蒙特卡洛算法：引入随机化策略，运行一次算法总能给出答案， 但未必正确， 可以肯定的是其正确性超过50%, 若运行多次，答案不变， 则该答案正确的可能 性非常高。 （蒙特卡洛算法可进行故障检测)