算法与程序(第五章)

蓝Q曦 included in 计算机算法设计与分析

2024-04-18 4122 words 9 minutes

回溯法

当需要找出问题的解集或者要求满足某些约束条件的最优解时，常使用回溯法
回溯法的基本方法就是搜索，是一种组织得井井有条的，能避免不必要搜索的穷举式搜索法
这种方法适用于解一些组合数相当大的问题，如排列、子集。0-1背包问题、n皇后安排问题等可以使用回溯法
回溯法在问题的解空间树中，按深度优先策略，从根结点出发搜索整个解空间树
算法搜索至解空间树的任意一结点时，先判断该结点是否包含问题的解
如果不包含，跳过对该结点为根的子树的搜索，返回该结点的父结点，继续对该结点兄弟结点的搜素（若有）。否则，进入该子树，继续按深度优先策略搜索
问题的解向量：回溯法希望一个问题的解能够表示成一个n元组 (x1,x2,…,xn)

0-1背包问题n元组？

xi取0或1组成的n元组

显约束：对分量xi的取值限定。
隐约束：为满足问题的解而对不同分支施加的约束。
解空间：对于问题的一个实例，解向量满足显式约束条件的所有n元组，构成了该实例的一个解空间。组织成一棵树 $\Rightarrow$解空间树

注意：同一个问题可能有不同的解空间树表示，有些表示方法更简单，解空间更小，搜索方法更快。

扩展结点一个正在产生儿子的结点称为扩展结点
活结点:一个自身已生成但其儿子还没有全部生成的结点称做活结点
死结点:一个所有儿子已经产生的结点称做死结点
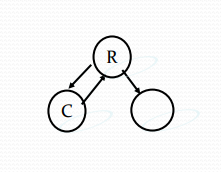
深度优先的问题状态生成法（演示）：

如果对一个扩展结点R，一旦产生了它的一个儿子C，就把C当做新的扩展结点，R成为活结点。在完成对子树C（以C为根的子树）的穷尽搜索之后，将R重新变成扩展结点，继续生成R的下一个儿子（如果存在）。 R的全部孩子结点产生完毕，R成为死结点。

宽度优先的问题状态生成法：在一个扩展结点变成死结点之前，它一直是扩展结点（第六章内容）
回溯法为了避免生成那些不可能产生最佳解的问题状态，要不断地利用剪枝函数来处死那些实际上不可能产生所需解或最优解的儿子结点，以减少问题的计算量。
具有剪枝函数的深度优先生成树法称为回溯法

回溯法的基本思想

针对所给问题，定义问题的解空间(所有可能的解集合）
确定易于搜索的解空间结构（树）；
以深度优先方式搜索解空间，并在搜索过程中用剪枝函数避免无效搜索。

常用剪枝函数：

用约束函数在扩展结点处剪去不满足约束的子树；

用限界函数剪去得不到最优解的子树

回溯法解题的一个显著特征是：在搜索过程中动态产生问题的解空间树，即边搜索边扩展分支。

(不同于数据结构中树的深度遍历方法，先创建树，再深度遍历）

在任何时刻，算法只保存从根结点到当前扩展结点的路径。

若解空间树中从根结点到叶结点的最长路径的长度为h(n)，则回溯法所需的计算空间通常为O(h(n))。

显式地存储整个解空间则需要$O(2^{h(n)})$或O(h(n)!)的内存空间

递归回溯算法框架

回溯法对解空间作深度优先搜索，一般用递归算法实现回溯法。

void backtrack (int t)
{
	if (t>n) output(x);
	else
		for (int i=f(n,t);i<=g(n,t);i++)
		{
			x[t]=h(i);
			if (constraint(t)&&bound(t)) 
				backtrack(t+1);
		}
}

当前扩展结点依次生成其各孩子结点，并记住路径信息，如果孩子结点满足约束条件和限界条件，则继续搜索孩子结点为根的子树（递归调用）

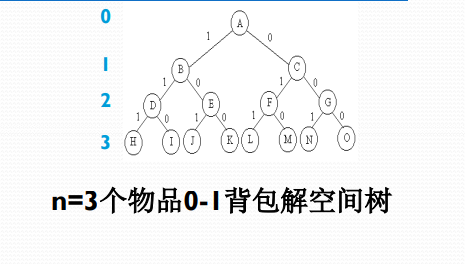
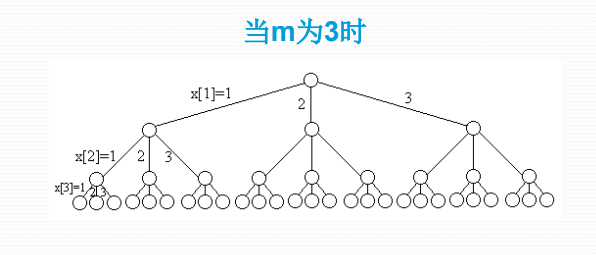
子集树与排列树的回溯算法框架

遍历子集树需$O(2^n)$计算时间

void backtrack (int t)
{
if (t>n) output(x);
 else
  for (int i=1;i>=0;i--) {
   x[t]=i;
   if (legal(t)) backtrack(t+1);
 	}
}

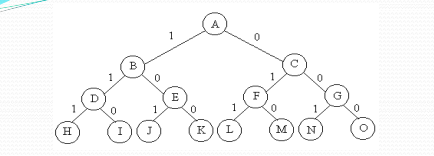
遍历排列树需要O(n!)计算时间

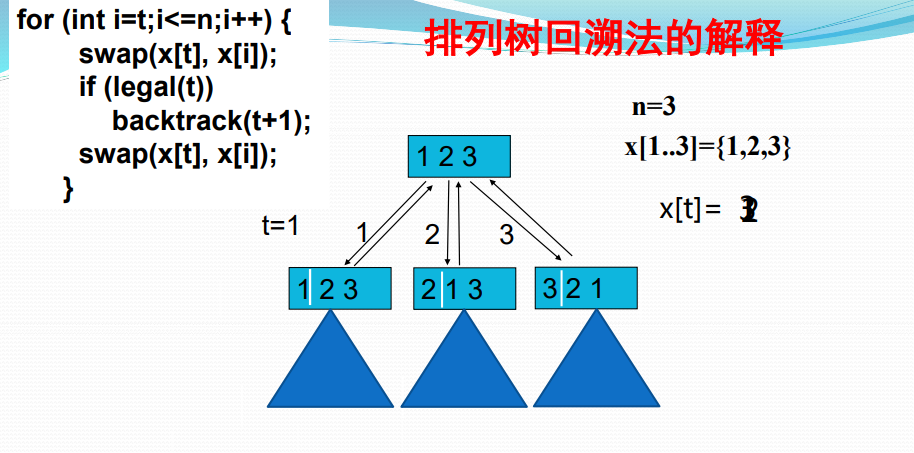
void backtrack (int t)
{
 if (t>n) output(x);
  else
   for (int i=t;i<=n;i++) {
    swap(x[t], x[i]);
    if (legal(t)) backtrack(t+1);
    swap(x[t], x[i]);
  }
}

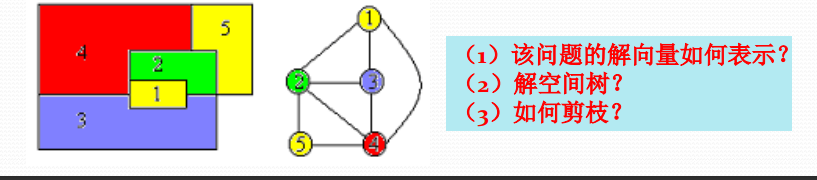
装载问题

共n个集装箱要装上2艘载重量分别为c1和c2的轮船，其中集装箱i的重量为wi，且 $\stackrel{n}{\sum\limits_{i=1}} w_i \leq c_i+c_2$ 。装载问题要求确定是否有一个合理的装载方案可将这些集装箱装上这2艘轮船。如果有，找出一种装载方案

最优装载方案：

首先将第一艘轮船尽可能装满；
将剩余的集装箱装上第二艘轮船

将第一艘轮船尽可能装满等价于选取全体集装箱的一个子集，使该子集中集装箱重量之和最大。

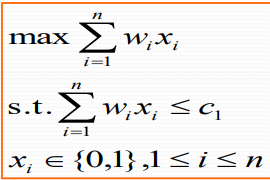
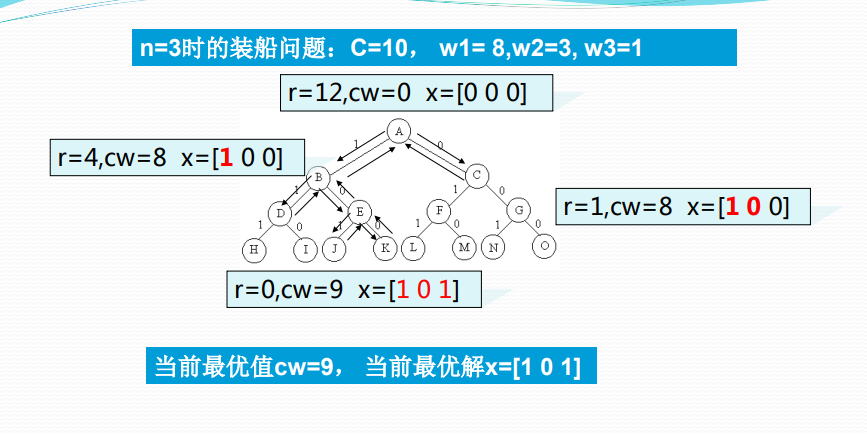
以3个集装箱装船为例

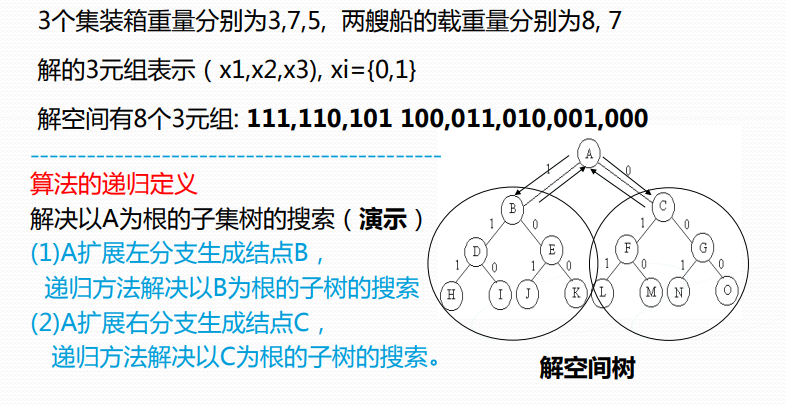
用回溯法解装载问题的时间复杂性是O(2n)。在某些情况下该算法优于动态规划算法。

回溯法算法如何计算其复杂性呢？

计算出解空间树中除叶子层之外的结点总数f(n)
每个非叶子结点搜索其下一层所有分支的时间复杂性（分、合）g(n)，
复杂性为O（f（n）*g(n)）

以最优装载问题为例, $f（n）=2^n-1， g（n）=O（1）$，其时间复杂性为$O（2 ^n$）

也可用递归方程描述：T（n）=2T（n-1）+O（1），n>0, T(1)=1;

本章讨论时间复杂性只有理论意义，没有实际意义，因为计算的是在没有任何剪枝的情况下的时间复杂性，实际上效率要好很多。

批处理作业调度

n个作业集合{1,2,…,n}。每个作业先由机器1处理，再由机器2处理。作业i需要机器j的处理时间为$M_{ij}$。

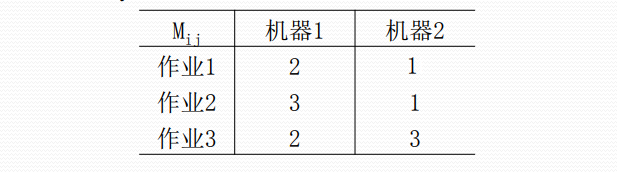
对于一个确定的作业调度，设Fij是作业i在机器j上完成的具体时间。

所有作业在机器2上完成的具体时间(时刻）之和f称为该作业调度的完成时间和。

要求：对于给定的n个作业，制定最佳作业调度方案(一个排列),使其完成时间和达到最小。(追求的是平均等待时间最小化)

3个作业的6种可能的调度方案是1,2,3；1,3,2；2,1,3；2,3,1； 3,1,2；3,2,1；它们所相应的完成时间和分别是19，18，20，21， 19，19。易见，最佳调度方案是1,3,2，其完成时间和为18。

关于排列树的时间复杂性的讨论

一颗n层的解空间树；时间复杂性的递归定义是

符号三角形问题

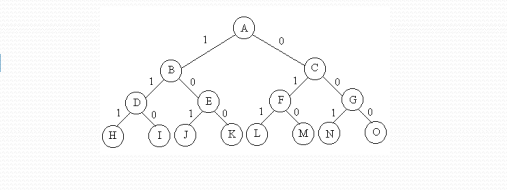
回溯法之符号三角形问题

n皇后问题

在n×n格的棋盘上放置彼此不受攻击的n个皇后。按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n后问题等价于在n×n格的棋盘上放置n个皇后，任何2个皇后不放在同一行或同一列或同一斜线上。

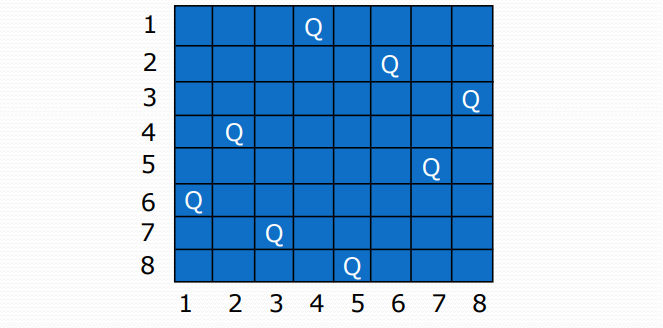
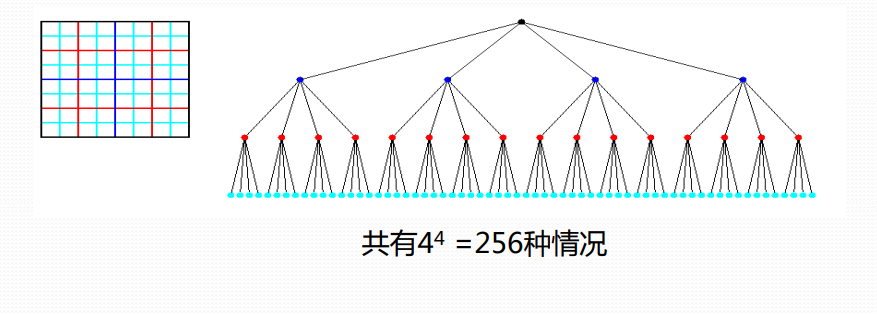
以n=4皇后问题为例

第一种：解空间是4叉树

每个皇后在一行上有四个可选位置（显约束：任两皇后不同行）

n后问题（n叉树）算法

解向量：($x_1 , x_2 , … , x_n$ )
显约束：$x_i$=1,2, … ,n 。任两皇后不同行
隐约束：(1)不同列：$x_i\neq x_j$ (2)不处于同一正\ 反对角线：$|i-j| \neq |x_i -x_j |$

bool Queen:Place(int k)
{
	for (int j=1;j<k;j++)
		if ((abs(k-j)==abs(x[j]- x[k])) ||(x[j]==x[k])) 
			return false;
		return true;
} 
void Queen::Backtrack(int t)
{
if (t>n) sum++;
else
	for (int i=1;i<=n;i++) {
		x[t]=i;
		if (Place(t)) Backtrack(t+1);
	}
}

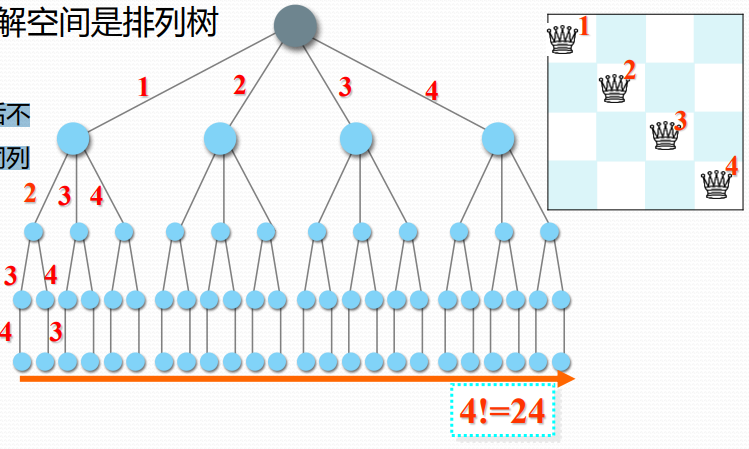
以n=4皇后问题为例

第二种:解空间是排列树

显约束：任两个皇后不同行、不同列

n后问题（排列树）算法

解向量：($x_1 , x_2 , … , x_n$ )

显约束：任两皇后不同行、不同列。x1x2….xn是1,2,….n排列

隐约束：不处于同一正\ 反对角线：$|i-j| \neq |x_i -x_j |$

bool Queen:Place(int k)
{
for (int j=1;j<k;j++)
	if (abs(k-j)==abs(x[j]-x[k])) 
		return false;
	return true;
} 
void Queen::Backtrack(int t)
{
if (t>n) sum++;
	else
	for (int i=t;i<=n;i++) {
		swap(x[t],x[i]);
		if (Place(t)) 
			Backtrack(t+1);
		swap(x[t],x[i]);
	}
}

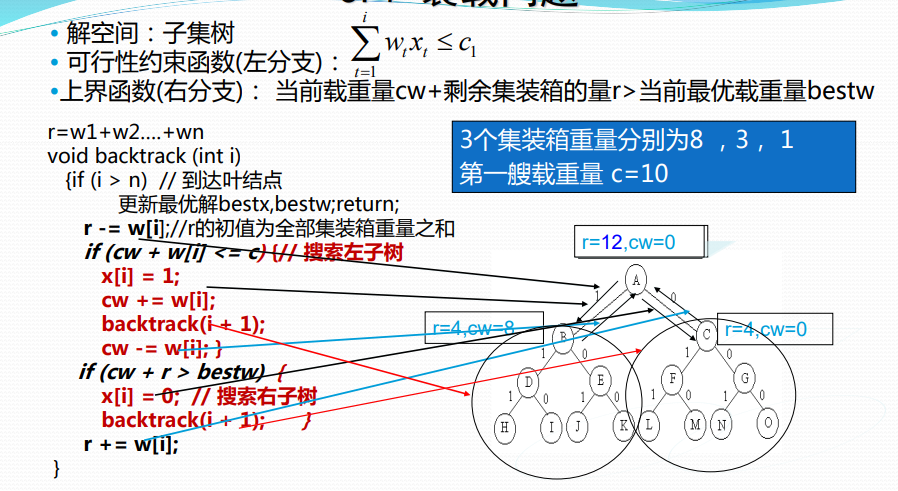
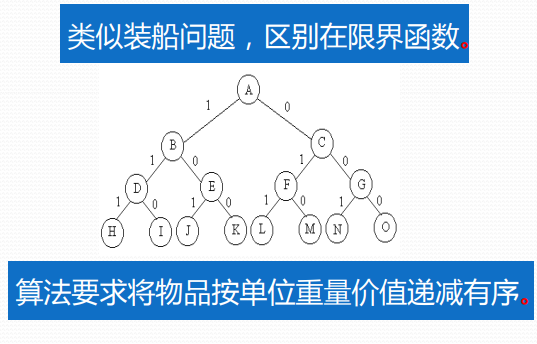
0-1背包问题

解空间：子集树

可行性约束函数:$\stackrel{n}{\sum\limits_{i=1}} w_ix_i \leq c_i$

void Backtrack(int i)
{if (i>n) {//到达叶节点
	bestp=cp； return；}
if（cw+w[i]<=c){\\进入左子树
	cw+=w[i];
	cp+=p[i];
	Backtrack(i+1);
	cw-=w[i];
	cp-=p[i];}
if(Bound(i+1)>bestp)\\进入右子树
	Backtrack(i+1);
}

限界函数：Bound（i）

template<class Typew, class Typep> 
Typep Knap<Typew, Typep>::Bound(int i)
{// 计算上界
Typew cleft = c - cw; // 剩余容量, cw当前在背包中物品重量
Typep b = cp; //cp当前在背包中物品价值
// 以物品单位重量价值递减序装入物品
while (i <= n && w[i] <= cleft) {
	cleft -= w[i];
	b += p[i];
	i++;
}
// 装满背包
if (i <= n) b += p[i]/w[i] * cleft;
return b;
}

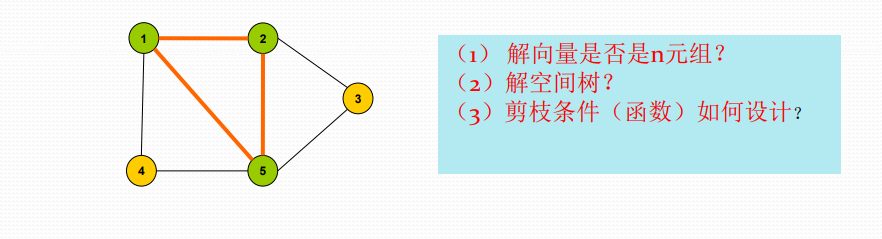
最大团问题

给定无向图G=(V，E)。如果UV，且对任意u，vU，有(u，v)E，则称U是G的完全子图。

完全子图U是G的团当且仅当U不包含在G的更大的完全子图中。

G的最大团是指G中所含顶点数最多的团。

解空间：子集树

可行性约束函数：顶点i到已选入的顶点集中每一个顶点都有边相连。

上界函数:有足够多的可选择顶点使得算法有可能在右子树中找到更大的团

void backtrack(int i)
{ if (i > n) {// 到达叶结点
	for (int j = 1; j <= n; j++) bestx[j] = x[j];
	bestn = cn; return; }
	// 检查顶点 i 与当前团的连接
	boolean ok = true;
	for (int j = 1; j < i; j++)
		if (x[j] == 1 && !a[i][j]) {// i与j不相连
			ok = false; break; }
if (ok) {// 进入左子树
	x[i] = 1; cn++;
	backtrack(i + 1);
	cn--; }
if (cn + n - i > bestn) {// 进入右子树
	x[i] = 0;
	backtrack(i + 1); } 
}

复杂度分析 最大团问题的回溯算法backtrack所需的计算时间显然为$O(n2^n )$。

图的m着色问题

给定无向连通图G和m种不同的颜色。用这些颜色为图G的各顶点着色，每个顶点着一种颜色。是否有一种着色法使G中每条边的2 个顶点着不同颜色。这个问题是图的m可着色判定问题。若一个图最少需要m种颜色才能使图中每条边连接的2个顶点着不同颜色，则称这个数m为该图的色数。求一个图的色数m的问题称为图的m 可着色优化问题。

解向量：($x_1 , x_2 , … , x_n$ )表示顶点i所着颜色$x_i$

可行性约束函数：顶点i与已着色的相邻顶点颜色不重复。

void backtrack(int t)
{
if (t>n) sum++;
else
	for (int i=1;i<=m;i++) {
		x[t]=i;
		if (ok(t)) backtrack(t+1);
	}
}
boolean ok(int k)
{// 检查颜色可用性
for (int j=1;j<k;j++)
	if (a[k][j] && (x[j]==x[k])) return false;
return true;
}

圆排列问题

旅行售货员问题

旅行售货员问题-回溯法

回溯法效率分析

回溯算法的效率在很大程度上依赖于以下因素：

产生x[k]的时间；
满足显约束的x[k]值的个数；
计算约束函数constraint的时间；
计算限界函数bound的时间；
满足约束函数和限界函数约束的所有x[k]的个数。

好的剪枝函数能显著地减少所生成的结点数。但这样的剪枝函数往往计算量较大。因此，需要权衡3，4跟5重排原理对于许多问题而言，在搜索试探时选取x[i]的值顺序是任意的。在其他

重排原理

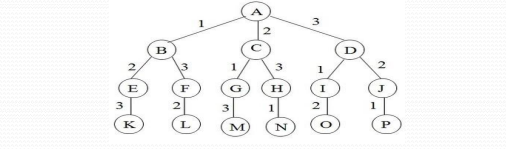
对于许多问题而言，在搜索试探时选取x[i]的值顺序是任意的。在其他条件相当的前提下，让可取值最少的x[i]优先。从图中关于同一问题的2棵不同解空间树，可以体会到这种策略的潜力。

图(a)，从第1层剪去1棵子树，则从所有应当考虑的3元组中一次消去12个3元组

图(b)，虽然同样从第1层剪去1棵子树，却只从应当考虑的3元组中消去8个3元组

回溯法小结

回溯法解决的问题，其解可以表示成n元组的形式。
确定易于求解的解空间树。常用：子集树、排列树、n叉树等

一个问题若有多种解空间树，评价：最后一层叶子结点的数量越少越好。
剪枝函数的设计：要求在保证剪枝效率的情况下计算尽量简单。

子集树：通常左分支使用约束函数、右分支使用限界函数剪枝。

排列树或n叉树：每个分支剪枝条件（函数）是相同的。
回溯法的套路：在递归调用backtrack（）前、后的代码动作是相反的
到达叶子结点时，通常一个新解就产生了。

如果是求最优解，你要确定需不需要跟之前的最优解比较来更新最优解。有些情况是必须要经过比较确认后才能更新为当前最优解。

Contents

算法与程序(第五章)

回溯法

回溯法

回溯法的基本思想

递归回溯算法框架

子集树与排列树的回溯算法框架

装载问题

批处理作业调度

关于排列树的时间复杂性的讨论

符号三角形问题

n皇后问题

以n=4皇后问题为例

n后问题（n叉树）算法

以n=4皇后问题为例

n后问题（排列树）算法

0-1背包问题

最大团问题

图的m着色问题

圆排列问题

旅行售货员问题

回溯法效率分析

重排原理

回溯法小结