算法与程序(第二章)
分治法
思想
分+治+合
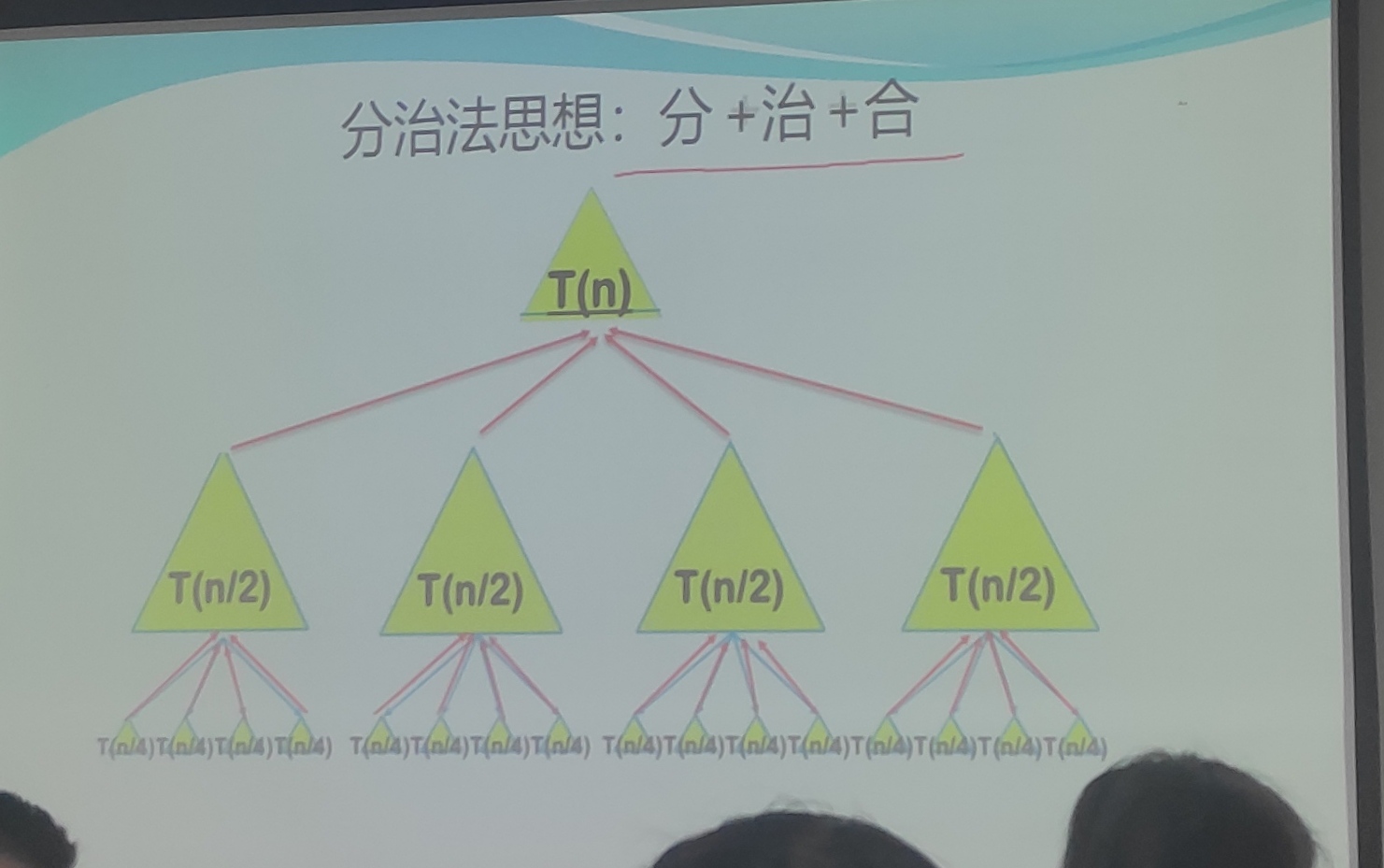
过程
-
分治法产生的子问题是原问题的较小模式
-
反复应用分治手段,可以使子问题规模不断减小
-
最终使子问题缩小到很容易直接求出其解
-
将规模较小问题的答案逐级向上合并(递归过程),可得大问题答案
分治法解决问题通常使用递归算法
递归的概念
直接或间接地调用自身的算法称为递归算法
递归算法的框架

要素
边界条件与递归方程是递归函数的两个要素 递归函数只有这两个要素才能在有限次运算得出结果
小结
优点:结构清晰,可读性强,而且容易用数学归纳法来证明算法的正确性,因此它为设计算法,调试程序带来很大方便
缺点:递归算法的运行效率较低,无论是耗费的计算时间还是占用的存储空间都比非递归算法要多
建议:
- 如果问题用递推方法可解决,就不要使用递归算法
- 用栈模拟的非递归算法,对运行效率改善有限,不建议使用
分治法的适用条件
n个问题分解为k个规模较小的子问题,子问题之间相互独立,不包含公共的问题,名子问题的解合并得到原问题的解
最优子传构性质
最优子结构是依赖特定问题和子问题的分割方式而成立的条件。各子问题具有最优解,就能求出整个问题的最优解,此时条件成立。
比如求广州到北京的最短距离,假设这个路径必经过中间的南京,那么先把路径分割为(广州,南京)和(南京,北京)。分别求出子路径的最短距离然后再连接,就可以得到广州到北京的最短路径。
因此,寻求最短路径的问题可以利用子路径的最优解获得整个问题的最优解。这样就可以证明,最短路径具有最优子结构。
分治法时间复杂度分析
一个分治法将规模为n的问题分成k个规模为n/m的子问题去解。为方便起见,设分解阈值n0为1,且adhoc解规模为1的问题耗费1单位时间。另外,将原问题分解为k个子问题及用merge将k个子问题的解合并为原问题的解需用f(n)单位时间
二分搜索技术
将n个元素分成个数大致相同的两半,取a[n/2]与x作比较。如果x=a[n/2],则找到x,算法终止;如果x<a[n/2],则只在数组a的左半部继续搜索x;如果x>a[n/2],则只在数组a的右半部继续搜索x
具体描述算法如下:

二分搜索技术(递归算法)
int BinarySearch_Rec(int num[], int target, int left, int right)
{
while (left <= right)
{
int mid = left + (right - left) / 2;
if (num[mid] == target)
return mid;
else if (num[mid] > target)
return BinarySearch_Rec(num, target, left, mid - 1);
else if (num[mid] < target)
return BinarySearch_Rec(num, target, mid + 1, right);
}
return -1;
}
算法复杂度分析
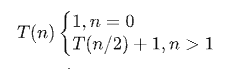
利用主定理或递归树可求其时间复杂性为:O(logn)
二分搜索技术(非递归算法)
int BinarySearch(int num[], int target, int len) //非递归实现
{
int left = 0;
int right = len - 1; // 第一个细节点
while (left <= right) // 第二个细节点
{
int mid = left + (right - left) / 2;
if (num[mid] == target)
return mid;
else if (num[mid] > target)
right = mid - 1; // 第三个细节点
else if (num[mid] < target)
left = mid + 1; // 第四个细节点
}
return -1;
}
算法复杂度分析
每执行一次while循环,待搜素数组的大小减小1/2.在最坏情况下,while循环被执行了O(logn)次,因此算法在最坏情况下计算时间复杂性为O(logn)
快速幂算法
给定实数a和非负整数n,用分治法设计求$a^n$的快速算法(递归算法)
分析:

算法如下
double exp2(double a,int n){
if(a==0)
return 0;
if(n<=0)
return 1;
else{
int x=exp2(a,n/2);
if(n%2)
return a*x*x;
else
return x*x;
}
}
该问题满足四个条件时间复杂性O(logn)
给定正整数a和n,用分治法设计求$a^n$的快速算法(非递归算法)
举例求$a^{93}$
n=93的二进制表示(如图),也就是n=64+16+8+4+1,因此$a^{93}=a^{64}a^{16}a^8a^4a$
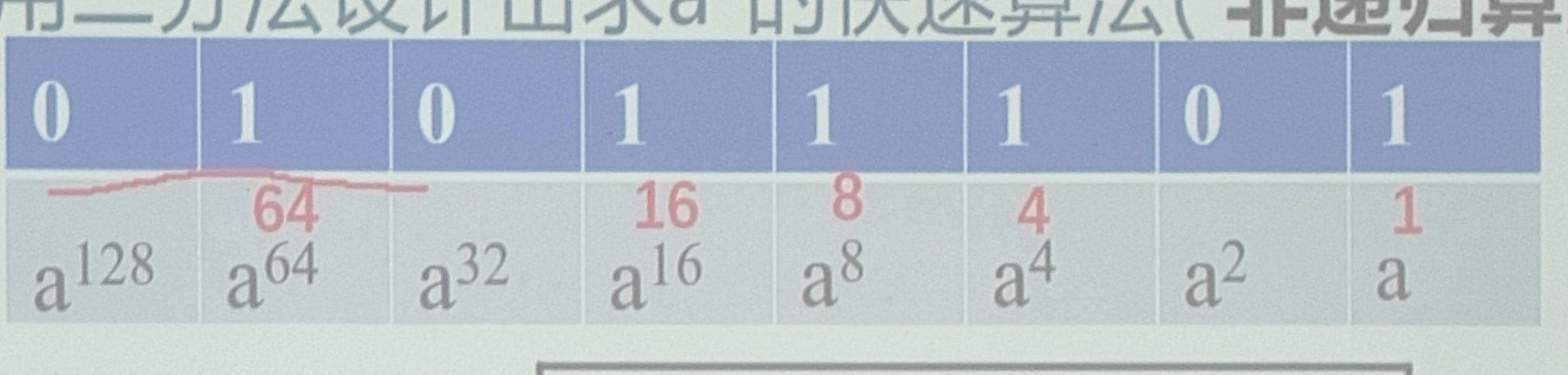
算法如下
double exp2(double a,int n){
int i;
double b,s=1.0;
i=n;
b=a;
while(i>0){
if(i%2)
s*=b;
i/=2;
b*=b;
}
return s;
}
Strassen矩阵乘法
首先,仍假设n是2的幂。将矩阵A,B和C中的每个矩阵都分块成4个大小相等的子矩阵,每个子矩阵都是n/2*n/2的方阵。由此可将方程C=AB重写为:
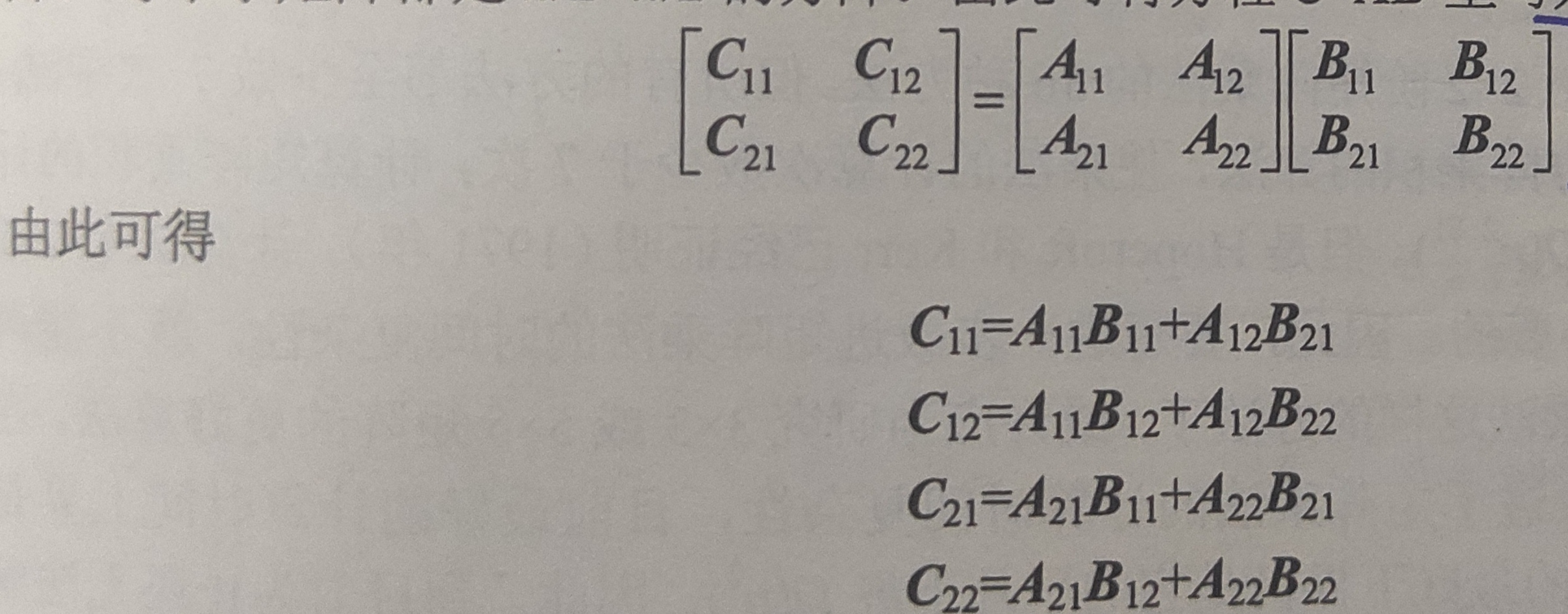
时间复杂性分析
上述分治法的计算时间耗费T(n)应满足
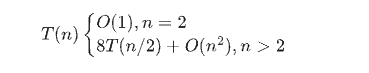
这个递归方程的解仍然是T(n)=O($n^3$)。因此,该方法并不比用原始定义直接计算更有效。究其原因,由于是该方法并没有减少矩阵的乘法次数。
要想改进矩阵乘法的计算时间复杂性,必须减少乘法运算
优化
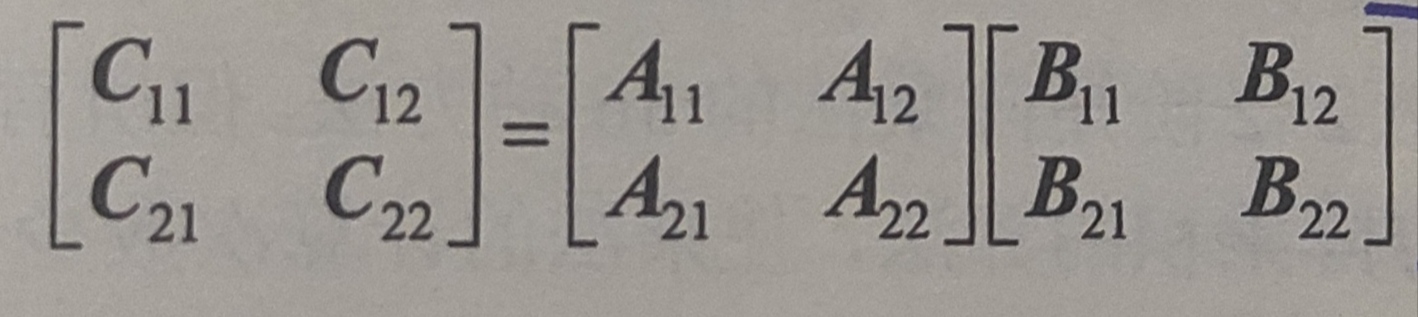

时间复杂性分析
Strassen矩阵乘法中用了7次对于n/2阶矩阵乘积的递归调用和18次n/2阶矩阵的加减运算。由此可知,该算法所需的计算时间T(n)满足如下递归方程:
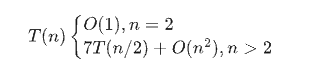
解此递归方程得T(n)=O($n^{log7}$)$\approx$O($n^{2.81}$)。由此可见,Strassen矩阵乘法的计算时间复杂性比普通矩阵乘法有较大改进
棋盘覆盖
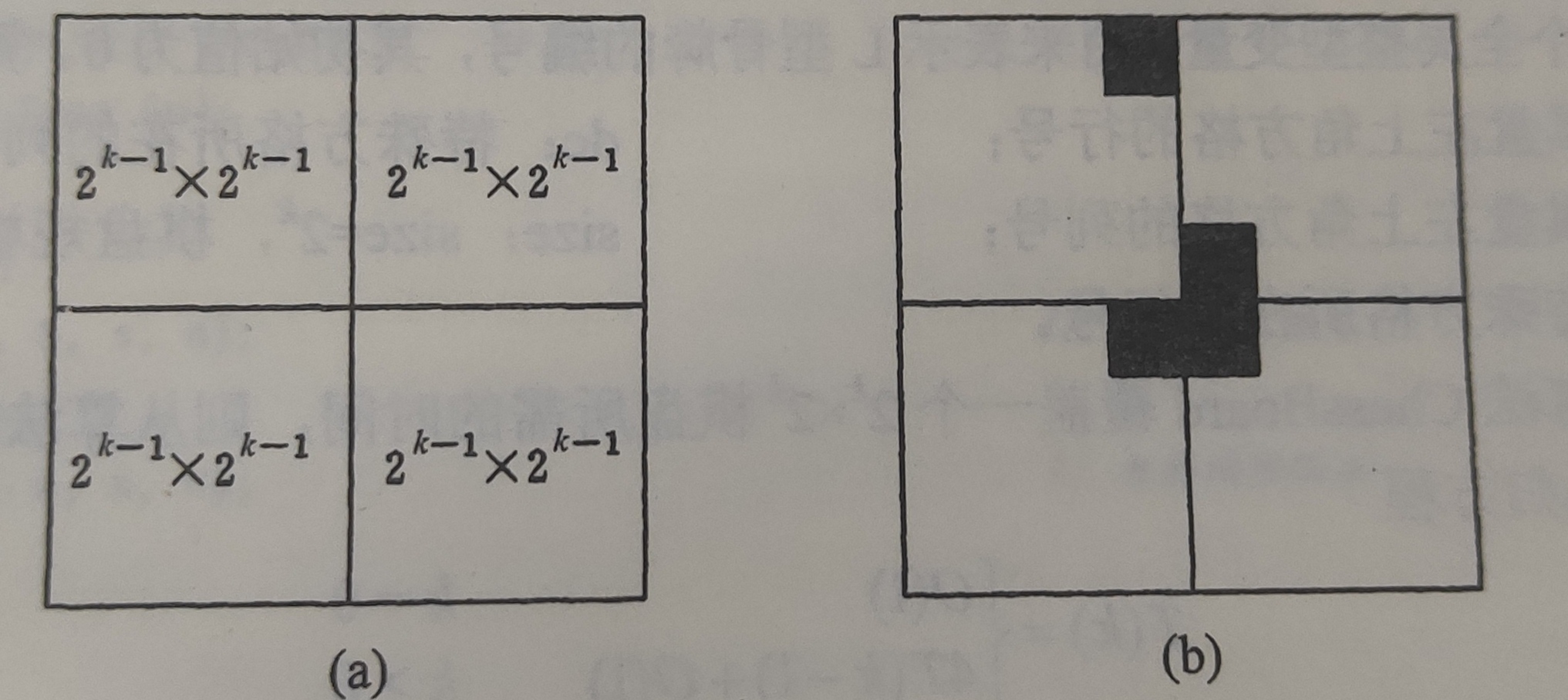
当k>0时,将$2^k\times 2^k$棋盘分割为4个$2^{k-1}\times 2{k-1}$子棋盘,如图a所示。特殊方格必位4个较小子棋盘之一中,其余3个子棋盘中无特殊方格。为了将这3个无特殊方格的子棋盘转化为特殊棋盘,可以用一个L型骨牌覆盖这3个较小棋盘的会合处,如b所示,这3个子棋盘上被L型骨牌覆盖的方格就成为该棋盘上的特殊方格,从而将原问题转化为4个较小规模的棋盘覆盖问题。递归地使用这种分割,直至棋盘简化为$1\times1$棋盘
算法如下
void chessBoard(int tr, int tc, int dr, int dc, int size)
{
if (size==1)
return;
int s = size/2; //分割棋盘
int t = ++num; //L型骨牌号
//覆盖左上角子棋盘
if (dr < tr + s && dc < tc +s)
{
//特殊方格在此棋盘中
chessBoard(tr,tc,dr,dc,s);
}
else //此棋盘中无特殊方格
{
//用t号L型骨牌覆盖右下角
Matrix[tr+s-1][tc+s-1] = t;
//覆盖其余方格
chessBoard(tr,tc,tr+s-1,tc+s-1,s);
}
//覆盖右上角子棋盘
if (dr < tr + s && dc >= tc + s )
{
//特殊方格在此棋盘中
chessBoard(tr,tc+s,dr,dc,s);
}
else //此棋盘中无特殊方格
{
//用t号L型骨牌覆盖左下角
Matrix[tr+s-1][tc+s] = t;
//覆盖其余方格
chessBoard(tr,tc+s,tr+s-1,tc+s,s);
}
//覆盖左下角子棋盘
if (dr >= tr + s && dc < tc + s)
{
//特殊方格在此棋盘中
chessBoard(tr+s,tc,dr,dc,s);
}
else
{
//用t号L型骨牌覆盖右上角
Matrix[tr+s][tc+s-1] = t;
//覆盖其余方格
chessBoard(tr+s,tc,tr+s,tc+s-1,s);
}
//覆盖右下角子棋盘
if (dr >= tr + s && dc >= tc + s)
{
//特殊方格在此棋盘中
chessBoard(tr+s,tc+s,dr,dc,s);
}
else
{
//用t号L型骨牌覆盖左上角
Matrix[tr+s][tc+s] = t;
//覆盖其余方格
chessBoard(tr+s,tc+s,tr+s,tc+s,s);
}
}
复杂度分析
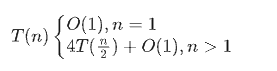
T(n)=O($n^2$)
本算法可使用队列或者栈实现,非递归算法
合并排序
将待排序元素分成大小大致相同的两个子集合,分别对两个子集合进行排序,最终将排好序的子集合合并成要求好的排好序的集合
算法描述(可递归)
template<class Type>
void MergeSort(Type a[],int left,int right){
if(left<right){ //至少有2个元素
int i =(left + right)/2; //取中点
MergeSort(a,left,i);
MergeSort(a,i+1,right);
Merge(a,b,left,i,right); //合并到数组b
Copy(a,b,left,right); //复制回数组a
}
}
算法MergeSort的递归过程可以消去
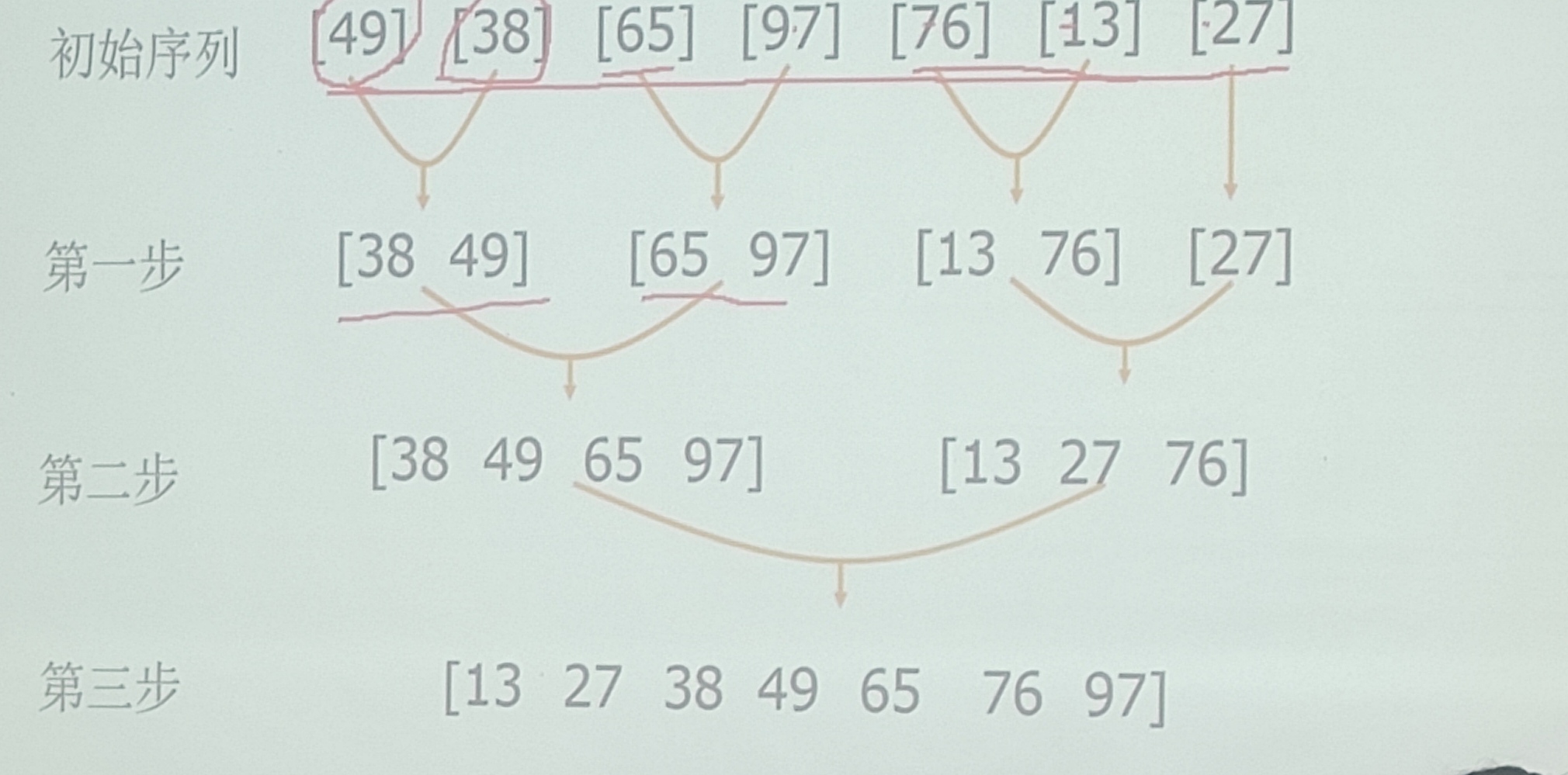
复杂度分析
最坏时间复杂度:O(nlogn)
平均时间复杂度:O(nlogn)
辅助空间:O(n)
稳定性:稳定
快速排序
快速排序算法是基于分治策略的另一个排序算法。其基本思想是,对于输入的子数组a[p:r],按以下三个步骤进行排序。
- 分解(Divide):以a[p]为基准元素将a[p:r]划分成3段a[p:q-1],a[q]和a[q+1:r],使a[p:q-1]中任何一个元素小于等于a[q],而a[q+1:r]中任何一个元素大于等于a[q]。下标q在划分过程中确定
- 递归求解(Conquer):通过递归调用快速排序算法,分别对a[p:q-1]和a[q+1:r]进行排序
- 合并(Merge):由于对a[p:q-1]和a[q+1:r]的排序是就地进行的,因此在a[p:q-1]和a[q+1:r]都已排好的序后,不需要执行任何计算,a[p:r]则已排好序
算法如下:
template(class Type)
void QuickSort(Type a[],int p,int r){
if(p<r){
int q=Partition(a,p,r);
QuickSort(a,p,q-1); //对左半段排序
QuickSort(a,q+1,r); //对右半段排序
}
}
对含有n个元素的数组a[0:n-1]进行快速排序只要调用QuickSort(a,0,n-1)即可。
上述算法中的函数Partition()以一个确定的基准元素a[p]对子数组a[p:r]进行划分,它是快速排序算法的关键。
算法如下:
template<Class Type>
int Partition (Type a[],int p,int r){
int i =p,j=r+1;
Type x =a[p];
//将小于x的元素交换到左边区域,将大于x的元素交换到右边区域
while(true){
while(a[++i]<x&&i<r);
while(a[--j]>x);
if(i>=j)
break;
Swap(a[i],a[j]);
}
a[p] = a[j];
a[j] = x;
return j;
}
复杂度分析
快速排序算法的性能取决于划分的对称性
最坏情况,每次划分出的二个子问题,一个长度为0,另一个长度为n-1,其对应的时间复杂性的递归定义为:
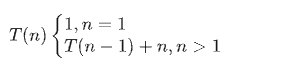
最坏时间复杂度:O($n^2$)
平均时间复杂度:O(nlogn)
稳定性:不稳定
通过修改算法partition,可以设计出采用随机选择策略的快速排序算法。可以在a[p:r]中随机选出一个元素作为划分基准。可以期望划分是较对称的。
template<Class Type>
int RandomizedPartition(Type a[],int p,int r){
int i = Random(p,r);
Swap(a[i],a[p]);
return Partition(a,p,r);
}
void RandomizedQuickSort(Type a[],int p,int r){
if(p<r){
int q=RandomizedPartition(a,p,r);
RandomizedQuickSort(a,p,q-1); //对左半段排序
RandomizedQuickSort(a,q+1,r); //对右半段排序
}
}
线性时间选择
给定线性序集中n个元素和一个整数k,$1\leq k \leq n$,要求找出这n个元素中第k小的元素
template<Class Type>
Type RandomizedSelect(Type a[],int p,int r,int k){
if(p==r)
return a[p];
int i=RandomizedPartition(a,p,r);
j=j-p+1;
if(j==k)
return a[i];
if(k<j)
return RandomizedSelect(a,p,i,k);
else
return RandomizedSelect(a,i+1,r,k-j);
}
时间复杂性分析
在最坏情况下,算法RandomizedSelect需要O($n^2$)计算时间
但可以证明,算法RandomizedSelect可以在O(n)平均时间内找出n个输入元素中的第k小元素
循环赛日程表
设计一个满足以下要求的比赛日程表
- 每个选手必须与其他n-1个选手各赛一次
- 每个选手一天只能赛一次;
- 循环赛一共进行 n−1 天
- 选手人数$n=2^k$
算法如下
void table(int[N][N],int i,int j,int n){ //i,j左上角行号列号,n为长度
if(n>1){
table(a,i,j,n/2);
table(a,i+n/2,j,n/2);
copy(a,i,j,i+n/2,j+n/2,n/2); //左上表拷贝至右下表
copy(a,i+n/2,j+n/2,n/2); //左下表拷贝至右上表
}
}
小结
- 在使用分治策略解决问题时,注意检查四个条件是否满足
- 尽量保证划分出的子问题规模大致一致。平衡子问题思想
- 如果可以使用递推的方式解决问题,尽量使用递推算法
- 递归的分治算法的时间复杂性分析,要先写出其时间复杂性的递归方程,然后用主定理或递归树解方程
- 用递归算法解决问题时,要分析出其边界条件和递归方程(过程)