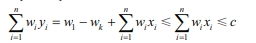算法与程序(第四章)
贪心算法
贪心算法的基本要素
贪心算法通过一系列选择来得到问题的解,所做的每个选择都是当前状态下局部最好选 择,即贪心选择。这种启发式的策略并不总能奏效,但在许多情况下确能达到预期目的。
从许多可以用贪心算法求解的问题中可以看到,它们一般具有两个重要的性质:贪心选择性质和最优子结构性质。
-
贪心选择性质
贪心选择性质是指,所求问题的整体最优解可以通过一系列局部最优的选择,即贪心选 择来达到。这是贪心算法可行的第一个基本要素,也是贪心算法与动态规划算法的主要区别。在动态规划算法中,每步所做的选择往往依赖于相关子问题的解。
-
最优子结构性质
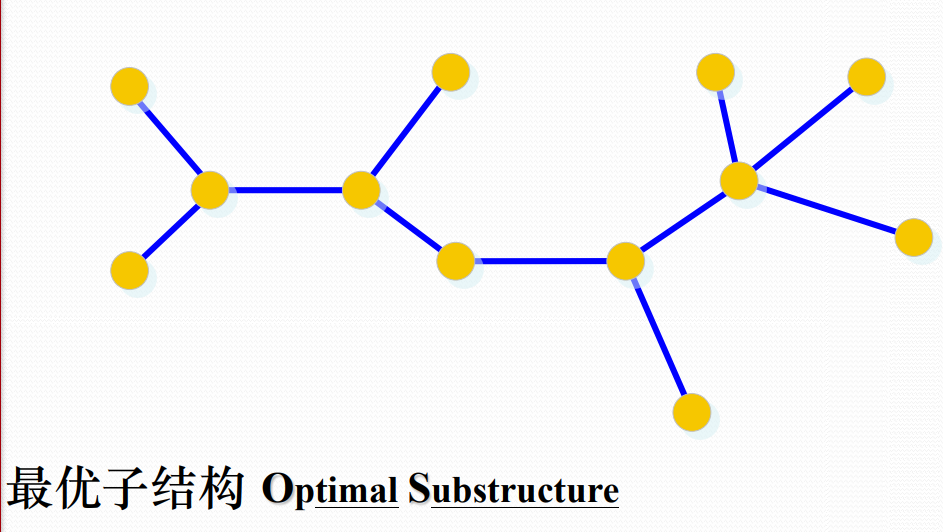
当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。问题的 最优子结构性质是该问题可用动态规划算法或贪心算法求解的关键特征
-
贪心算法与动态规划算法的差异
贪心算法和动态规划算法都要求问题具有最优子结构性质
0-1 背包问题
给定 n 种物品和一个背包。物品 i 的重量是 wi,其价值为 vi,背包的容 量为 c。问应如何选择装入背包中的物品,使得装入背包中物品的总价值最大?
在选择装入背包的物品时,对每种物品 i 只有两种选择,即装入背包或不装入背包。不 能将物品 i 装入背包多次,也不能只装入部分的物品 i
此问题的形式化描述是,给定 $c>0,w_i>0,v_i>0(1≤i≤n)$,要求找出一个 n 元的 0-1 向 量$(x_1, x_2, …, x_n)$,$x_i∈{0, 1}$,1≤i≤n,使得 $\stackrel{n}{\underset{i=1}{\sum}}w_ix_i \leq c$,而且 $\stackrel{n}{\underset{i=1}{\sum}}v_ix_i$达到最大
背包问题
与 0-1 背包问题类似,不同的是在选择物品 i(1≤i≤n)装入背包时,可以选择物品 i 的一部分,而不一定要全部装入背包
此问题的形式化描述是,给定 $c>0,w_i>0,v_i>0(1≤i≤n)$,要求找出一个 n 元向量$(x_1, x_2, …, x_n)(0≤x_i≤1,1≤i≤n)$,使得 $\stackrel{n}{\underset{i=1}{\sum}}w_ix_i \leq c$,而且 $\stackrel{n}{\underset{i=1}{\sum}}v_ix_i$达到最大。
这两类问题都具有最优子结构性质。
虽然这两个问题极为相似,但背包问题可以用贪心算法求解,而 0-1 背包问题不能用贪 心算法求解。用贪心算法解背包问题的基本步骤是
- 首先计算每种物品单位重量的价值 $v_i/w_i$;
- 依贪心选择策略,将尽可能多的单位重量价值最高的物品装入背包。
- 若将这种物品全部 装入背包后,背包内的物品总重量未超过 c,则选择单位重量价值次高的物品并尽可能多地 装入背包
- 算法结束
算法描述
void Knapsack(int n, float M, float v[], float w[], float x[]) {
Sort(n, v ,w);
int i;
for (i=1; i <= n; i++)
x[i] = 0;
float c = M;
for (i=1; i <= n; i++) {
if (w[i]>c)
break;
x[i] = 1;
c −= w[i];
}
if (i <= n)
x[i]=c/w[i];
}
算法 Knapsack 的主要计算时间在于,将各种物品依其单位重量的价值从大到小排序。 因此,算法的计算时间上界为 O(nlogn)。
最优装载
有一批集装箱要装上一艘载重量为 c 的轮船。其中集装箱 i 的重量为 wi。最优装载问题 要求在装载体积不受限制的情况下,将尽可能多的集装箱装上轮船
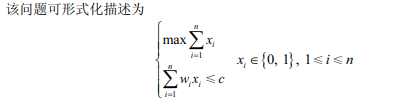
式中,变量 $x_i=0$ 表示不装入集装箱 i,$x_i=1$ 表示装入集装箱 i
-
算法描述
最优装载问题可用贪心算法求解。采用重量最轻者先装的贪心选择策略,可产生最优装 载问题的最优解。具体算法描述如下
template<class Type> void Loading(int x[], Type w[], Type c, int n) { int *t = new int [n+1]; Sort(w, t, n); for (int i=1; i <= n; i++) x[i]=0; for (int i=1; i <= n && w[t[i]] <= c; i++) { x[t[i]] = 1; c -= w[t[i]]; } } -
贪心选择性质
设集装箱已依其重量从小到大排序,$(x_1, x_2, …, x_n)$是最优装载问题的一个最优解,设$ k= \underset{1 \leq i \leq n}\min {i|x_i=1}$,如果给定的最优装载问题有解,则 1≤k≤n。
-
当 k=1 时,(x1, x2, …, xn)是一个满足贪心选择性质的最优解。
-
当 k>1 时,取 $y_1=1,y_k=0,y_i=x_i,1<i≤n,i≠k$,则

因此,$(y_1, y_2, …, y_n)$是所给最优装载问题的可行解。
另一方面,由 $\stackrel{n}{\underset{i=1}{\sum}}y_i=\stackrel{n}{\underset{i=1}{\sum}}x_i$ 知,$(y_1, y_2, …, y_n)$是满足贪心选择性质的最优解。所以,最优 装载问题具有贪心选择性质
该证明方法只证明了任何一个最优解都可以转换为第一个集装箱上船的最优解(满足贪心策略),此方法对于子问题同样有效,因此可将一个普通最优解转换为满足贪心策略的最优解
-
-
最优子结构性质
设$(x_1, x_2, …, x_n)$是最优装载问题的满足贪心选择性质的最优解,则 $x_1=1,(x_2, x_3, …, x_n)$ 是轮船载重量为 $c−w_1$、待装船集装箱为{2, 3, …, n}时相应最优装载问题的最优解。也就是 说,最优装载问题具有最优子结构性质。
哈夫曼编码
哈夫曼编码
单源最短路径
给定带权有向图G =(V,E),其中每条边的权是非负实数。V中的一个顶点,称为源。计算从源到所有其他各顶点的最短路径长度。
这个问题通常称为单源最短路径问题
路径长度是指路径上各边权之和。
-
算法基本思想
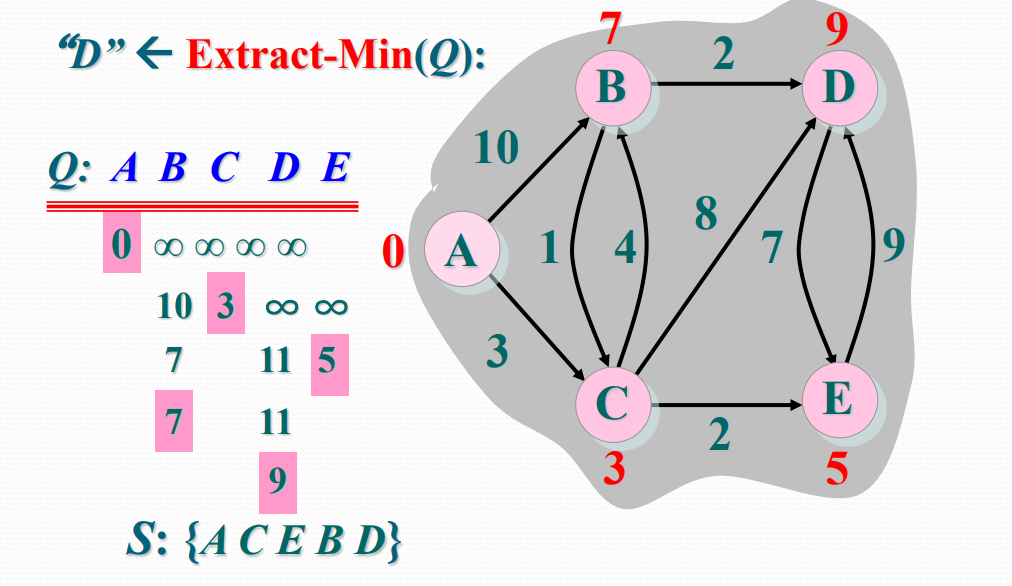
Dijkstra算法是解单源最短路径问题的贪心算法。
- 设置顶点集合S并不断地作贪心选择来扩充这个集合。一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知
- 初始时,S中仅含有源
- 从源只经过S中顶点到达u(S外)称为从源到u的特殊路径,用数组dist记录当前每个顶点的最短特殊路径长度。最短特殊路径长度最小的为最短路径已知。
- 每次从V-S中取出最短路径长度已知的顶点u,将u添加到S中,同时对数组dist作必要的修改。直到S包含了所有V中顶点
-
算法演示

-
算法的正确性和计算复杂性
- 贪心选择性质
- 最优子结构性质
- 计算复杂性
外循环需要执行n-1次(即n-1个顶点加入s集合)
内循环执行O(n)时间(更改最短特殊路径长度、找最短路径长度已知的顶点加入s)。
所以算法需要$O(n^2)$时间。
最小生成树
设G =(V,E)是无向连通带权图,即一个网络
E中每条边(v,w)的权为c[v][w]。
如果G的子图G’是一棵包含G的所有顶点的树,则称G’为G的生成树
生成树上各边权的总和称为该生成树的耗费
在G的所有生成树中,耗费最小的生成树称为G的最小生成树(Minimum Spanning Tree ),简称MST
-
最小生成树性质
用贪心算法设计策略可以设计出构造最小生成树的有效算法。Prim算法和Kruskal算法,这2个算法做贪心选择的方式不同,但它们都利用了最小生成树性质(贪心策略)
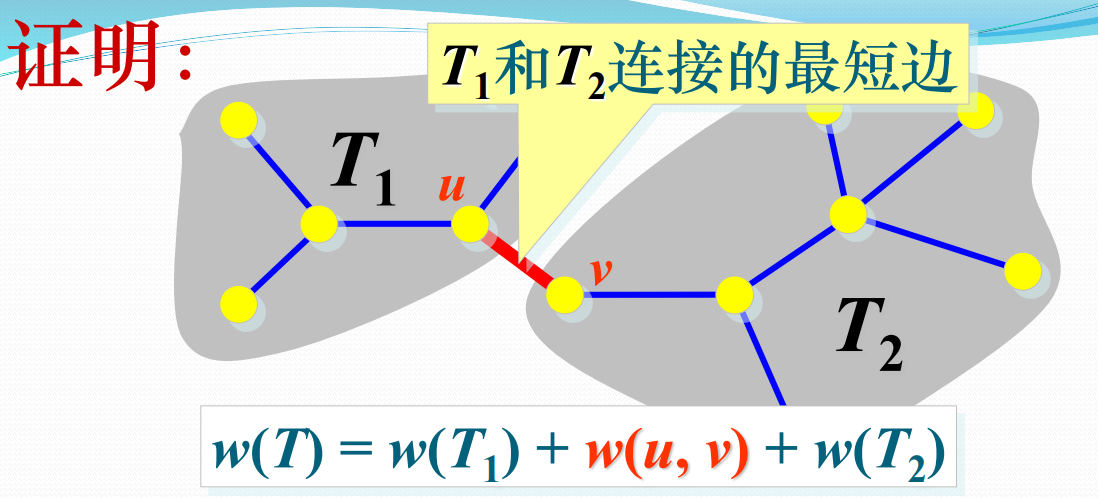
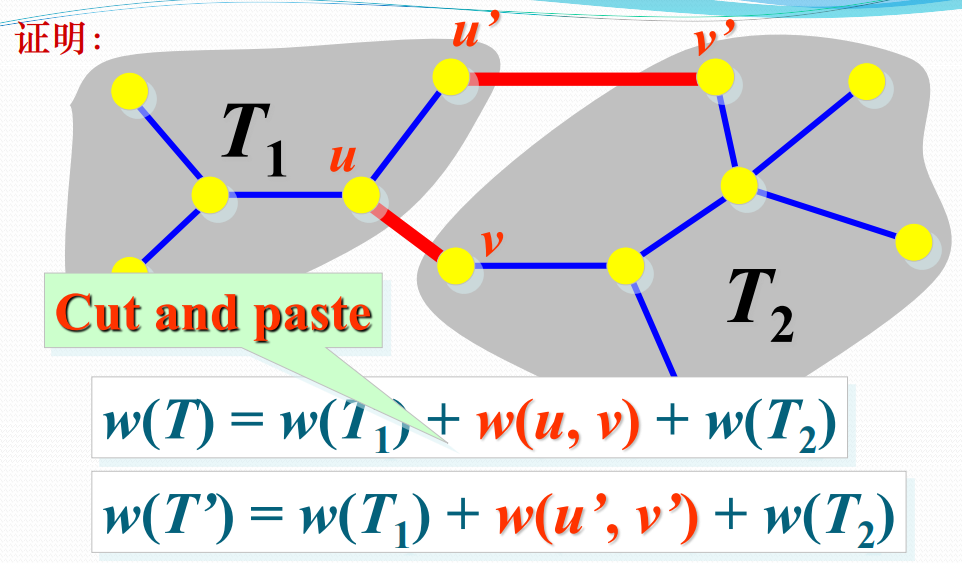
设G=(V,E)是连通带权图,U是V的真子集。如果$(u,v)\in E$,且$u\in U,v\in V-U$,且在所有这样的边中,(u,v)的权c[u][v]最小,那么一定存在G的一棵最小生成树,它以(u,v)为其中一条边。这性质有时也称为MST(最小生成树)性质。

-
MST在现实世界中应用非常广泛
- 交通
- 电信
- 网络通信
- 集成电路布线

-
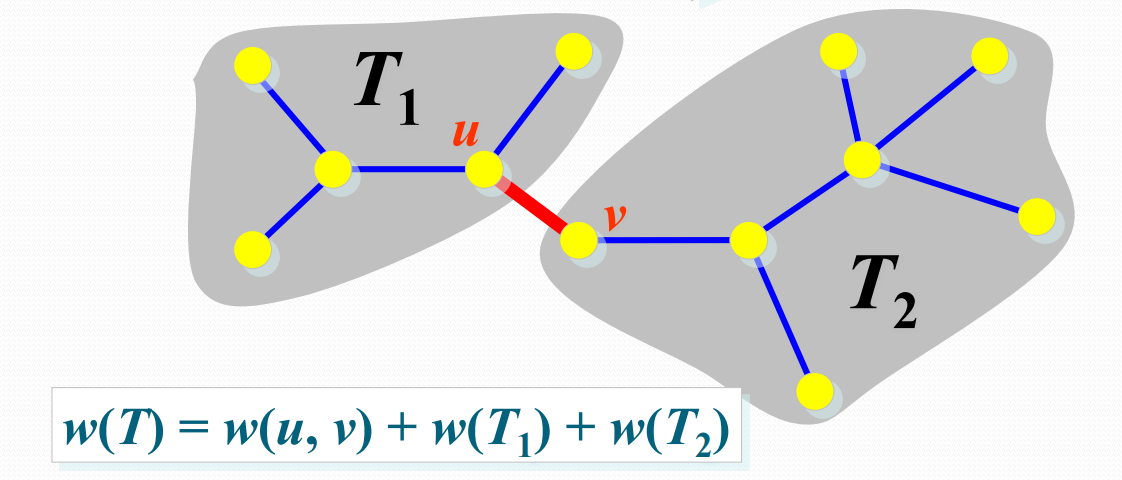
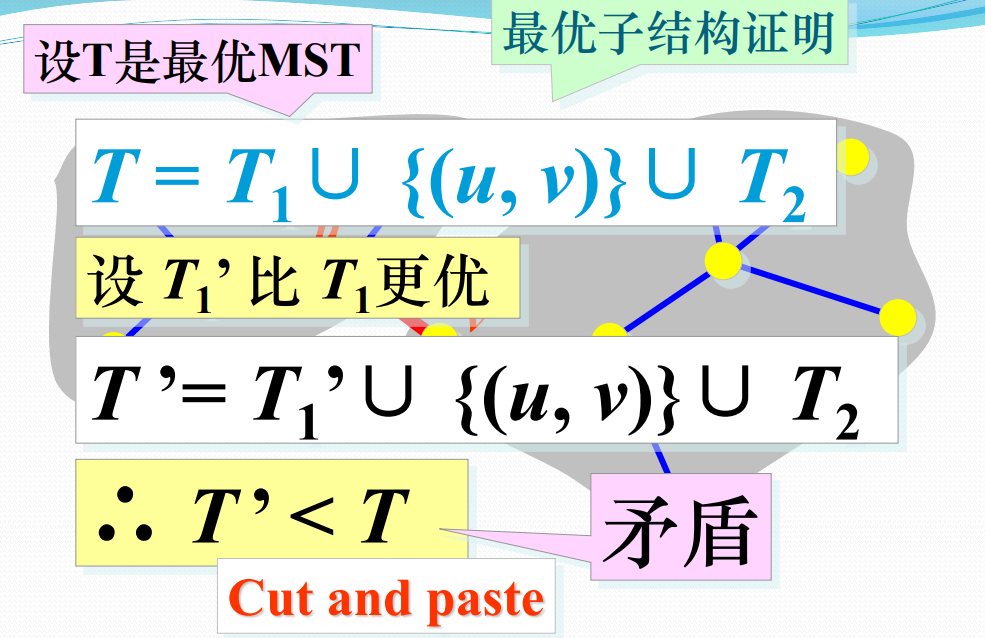
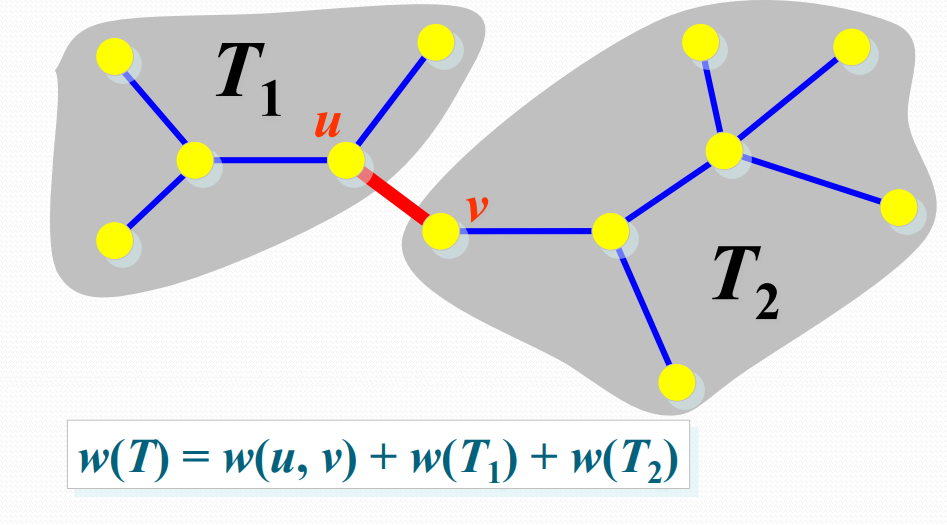
最优子结构证明



-
Prim算法(选顶点加入集合S)
设G=(V,E)是连通带权图,V={1,2,…,n}。
构造G的最小生成树的Prim算法的基本思想是:
- 首先置S={1},
- 然后,只要S是V的真子集,就作如下的贪心选择:选取满 足条件$i\in S,j\in V-S$,且c[i][j]最小的边,将顶点j添加到S中
- 这个过程一直进行到S=V时为止
在这个过程中选取到的所有边恰好构成G的一棵最小生成树
-
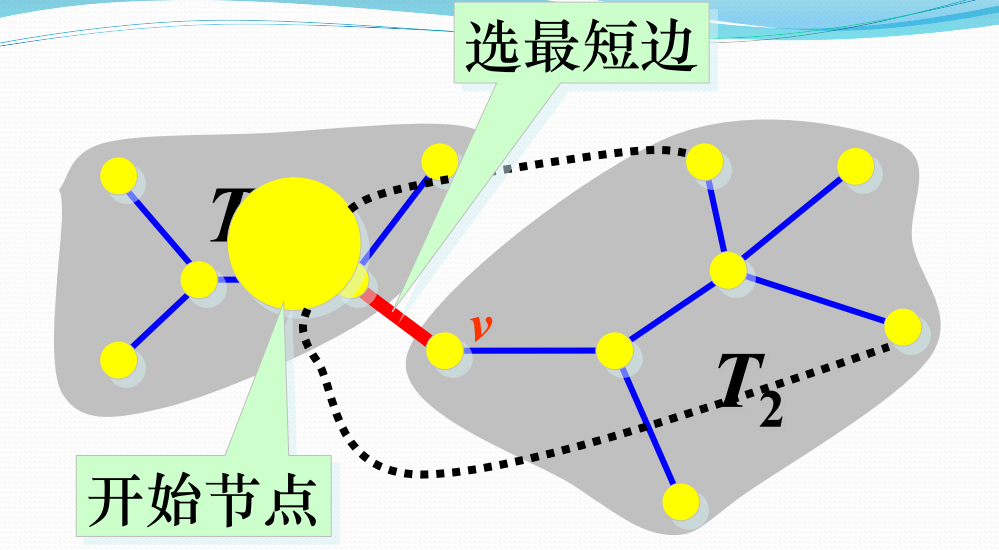
Kruskal算法(选择连接属于两个不同连通分支的最小边)
- 首先将G的n个顶点看成n个孤立的连通分支。
- 所有的边按权从小到大排序
- 顺序检查每条边,如果一条边的端点v和w分别是当前2个不同的连通 分支T1和T2,用边(v,w)将T1和T2连接成一个连通分支,否则放弃这条边。
- 该过程一直到只剩一个连通分支时为止(或者说选择了n-1条边为止)
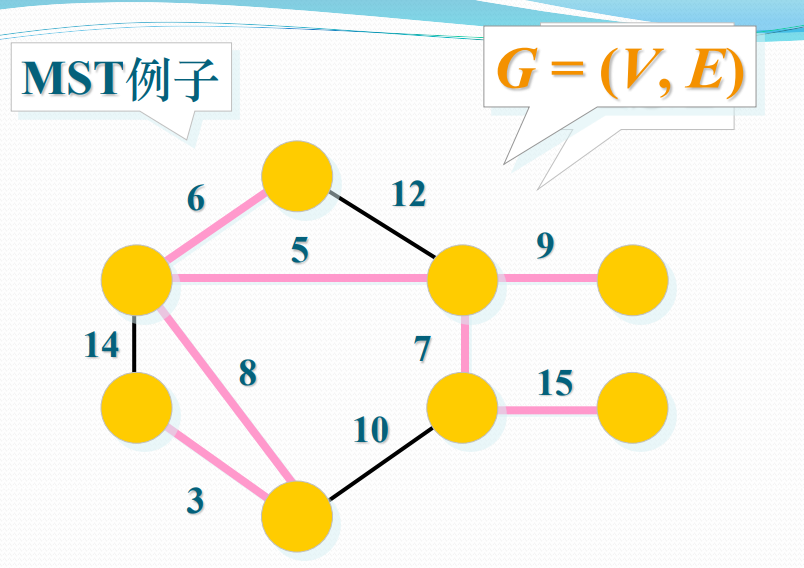
例如,对前面的连通带权图,按Kruskal算法顺序得到的最小生成树上的边如下图所示。

对比
当图的边数为e时,Kruskal算法所需的计算时间是 , Prim算法是O(n2)。 当 时,Kruskal算法比Prim算法差,但当 时,Kruskal算法却比Prim算法好得多。
贪心选择性质
局部最优即全局最优
证明
多机调度问题
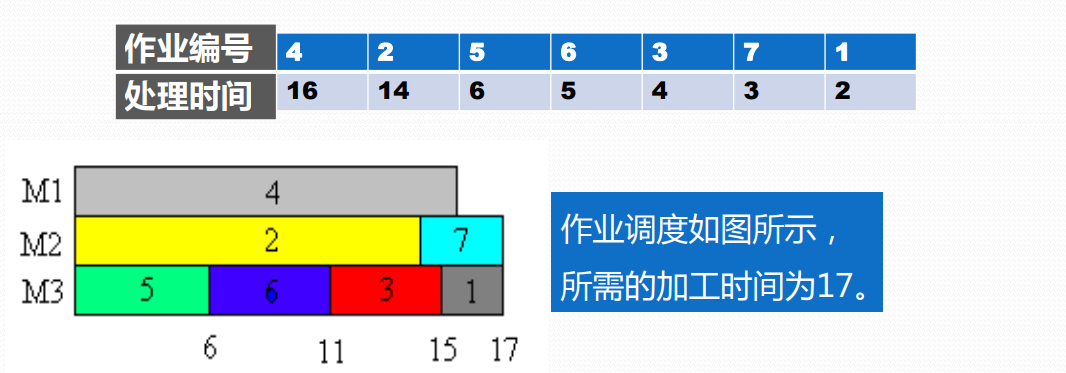
多机调度问题要求给出一种作业调度方案,使所给的n个作业在尽可能短的时间内由m台机器加工处理完成。
约定,每个作业均可在任何一台机器上加工处理,但未完工前不允许中断处理。作业不能拆分成更小的子作业
这个问题是NP完全问题,到目前为止还没有有效的解法。对于这一类问题,用贪心策略有时可以设计出较好的近似算法
采用最长处理时间作业优先的贪心选择策略可以设计出解多机调度问题的较好的近似算法
当 时$n \leq m$,只要将机器i的[0, ti]时间区间分配给作业i即可,算法只需要**O(1)**时间
当 时n>m,首先将n个作业依其所需的处理时间从大到小排序。然后依此顺序将作业分配给占用时间少的处理机。算法所需的计算时间为 O(nlogn)
例如,设7个独立作业{1,2,3,4,5,6,7}由3台机器M1,M2和M3加工处理。各作业所需的处理时间分别为{2,14,4,16,6,5,3}