算法与程序

算法

是满足下述性质的指令序列:

1. 输入:有零个或多个外部量作为算法的输入
2. 输出:算法产生至少一个量作为输出
3. 确定性:组成算法的每条指令是清晰的，无歧义的
4. 有限性:算法中每条指令的执行次数是有限的，执行每条指令的时间也是有限的

程序

与算法不同。程序是算法用某种程序设计语言的具体实现，程序可以不满足算法的性质

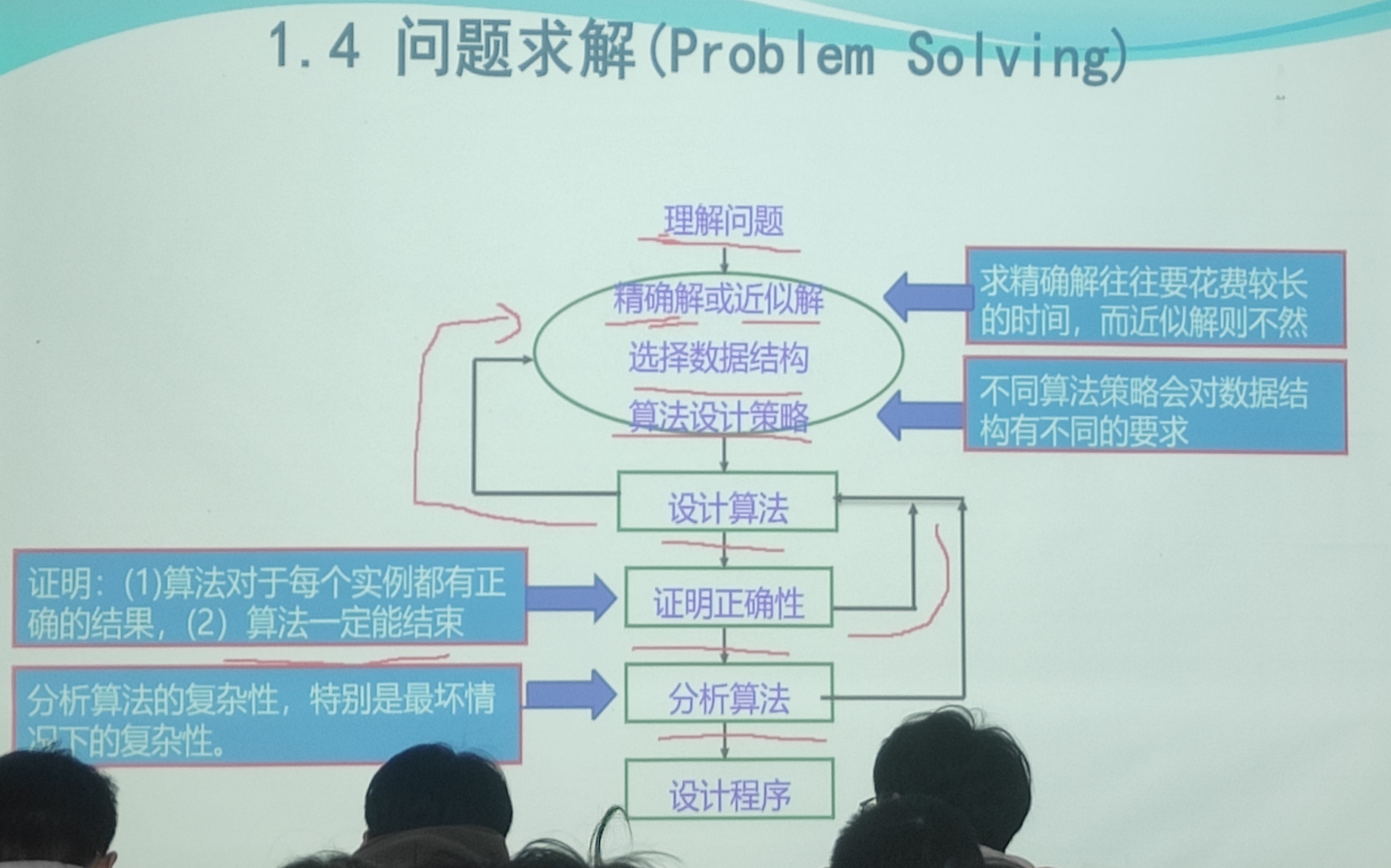
问题求解(图)

算法复杂性分析

时间复杂性

输入为ⅰ时的跟规模n相关的算法运行时间增长率

空间复杂性

输入为ⅰ时的跟规模n相关的算法辅助空间增长率

分析

算法复杂性分析→算法的能行性 n！，2n，n较大时 同一问题不同算法的算法复杂性分析→算法的优劣 时间复杂性与空间复杂性的分析方法类同，主要讨论时间复杂性

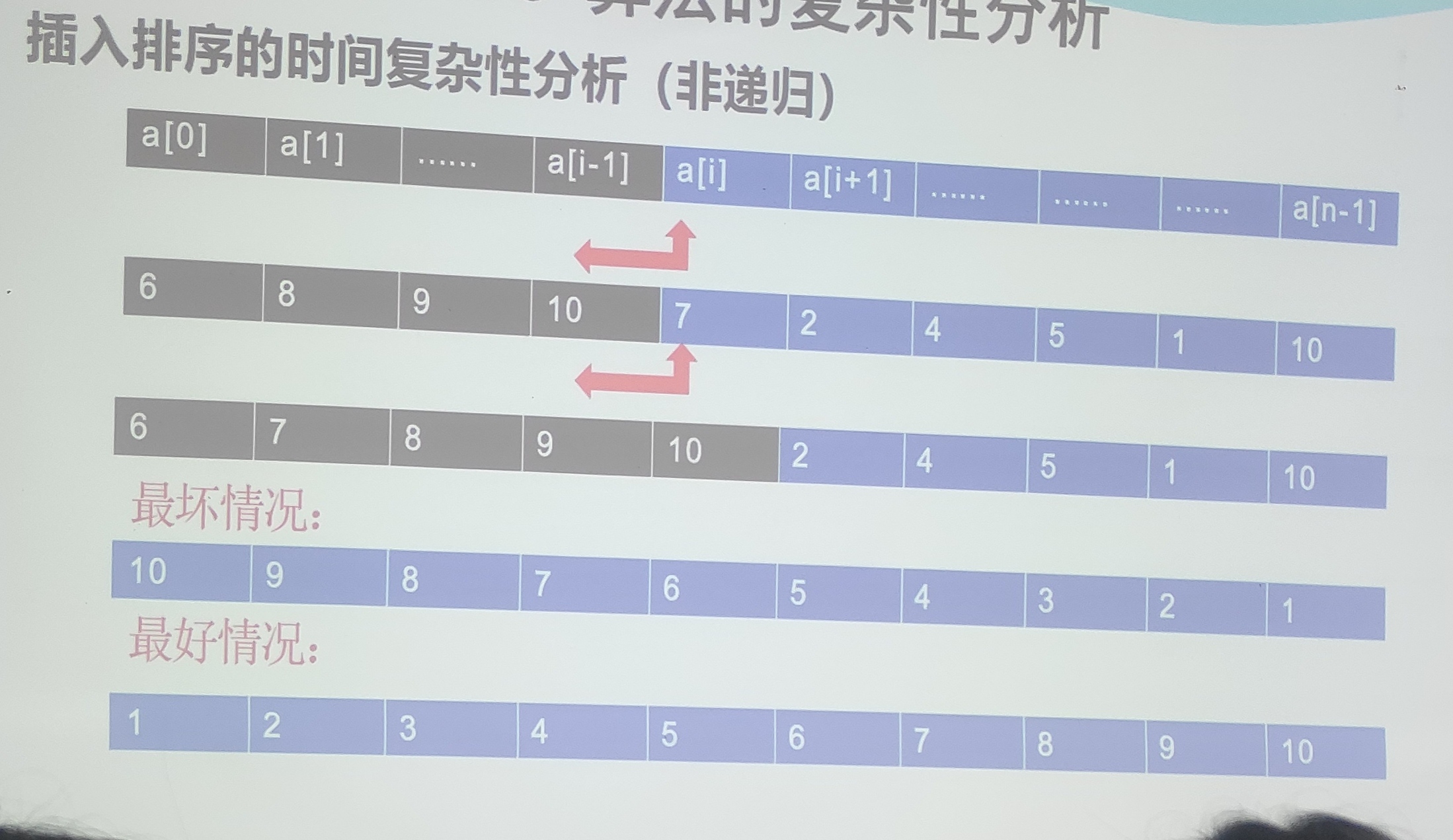
时间复杂性分析方法

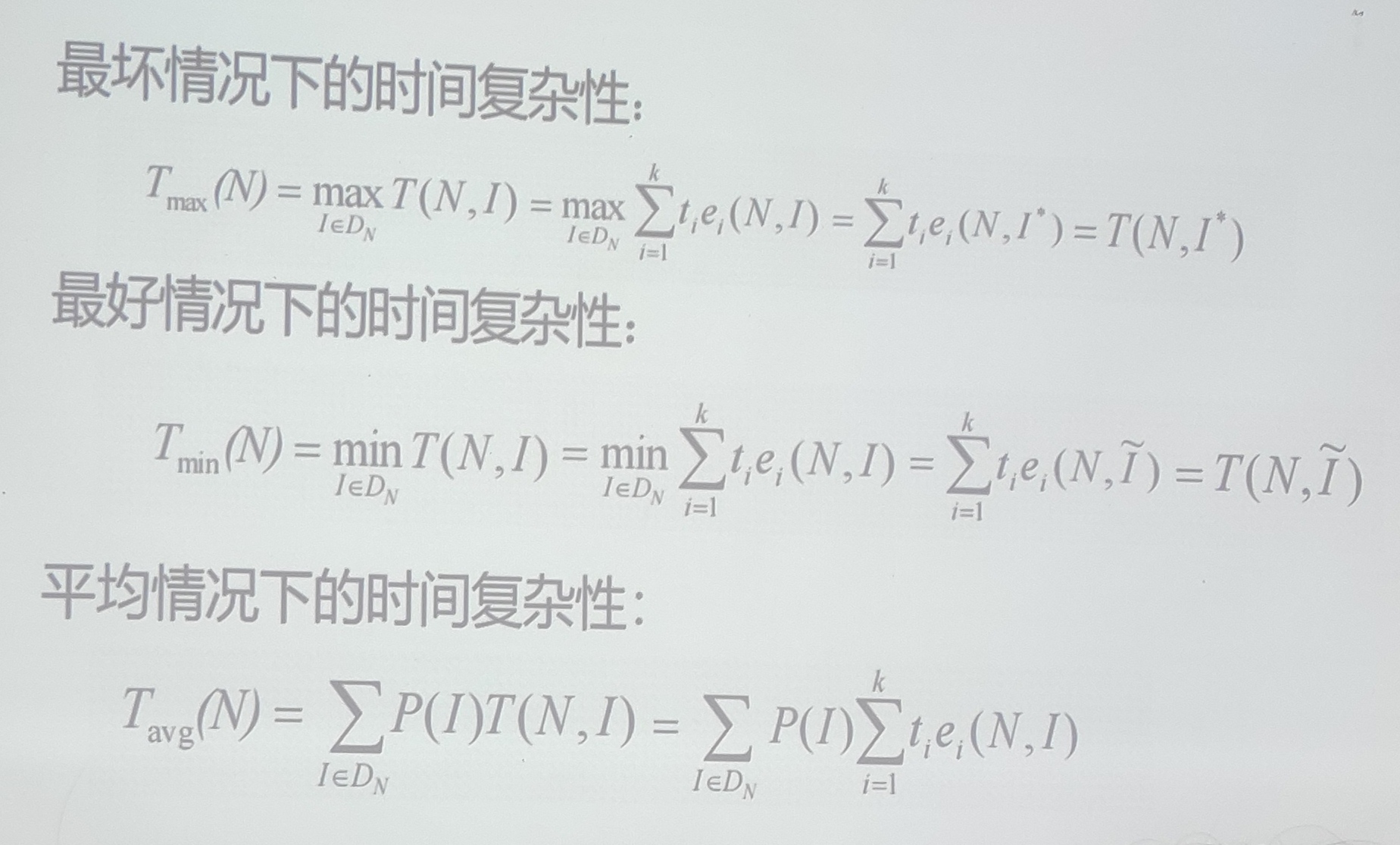
分类

1. 非递归算法的时间复杂性分析

2. 递归算法的时间复杂性分析

   

算法复杂性在渐近意义下的阶

渐近意义下的记号：O，Ω，θ，o，ω g(n)是定义在正数集上的正函数。T(n)为算法的时间复杂性

渐近上界记号O

若T(n) = O(g(n))

含义：算法在任何实例情况下，其时间复杂度的阶不超过g(n)的阶

即：$\lim_{n\rightarrow\infty}\frac{T_max(n)}{g(n)}=c\neq0$,c为常数

上例中 $\lim_{n\rightarrow\infty}\frac{T_max(n)}{n^2}=\frac{c4+c5+c6}{2}$为常数，故T(n)=O(n2)

记号θ

举例有一个算法A：

最坏情况：Tmax=c1n2+n+4

最好情况：Tmin=c2n2

存在g(n)=n2,有T(n) = Ω(g(n)) 和 T(n) = O(g(n))

因此 T(n) = θ(g(n))

非紧渐近上界记号 o

若T(n) = o(g(n))

含义：算法在任何实例情况下，其算法时间复杂性的阶小于g(n)的阶

即 $\lim_{n\rightarrow\infty}\frac{T_max(n)}{g(n)}=0$

举例：g(n) = n2,Tmax(n)=c2nlogn —> o(n2)

非紧渐近上界记号 ω

若T(n) = ω(g(n))

含义：算法在任何实例情况下，其算法时间复杂性的阶大于g(n)的阶

即 $\lim_{n\rightarrow\infty}\frac{T_min(n)}{g(n)}=\infty$

举例：g(n)=n,Tmin=c1nlogn—>ω(n)

简便分析方法

最优算法

Master定理方法求递归算法时间复杂性

第二章分治策略中，通常设计为递归算法

时间复杂性的递归定义一般有如下形式

例题

第二章棋盘覆盖的时间复杂性