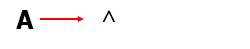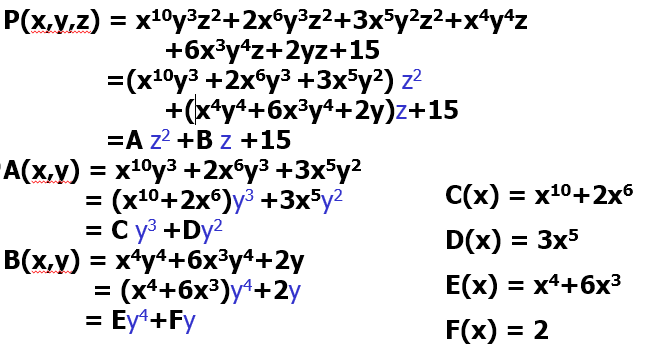数据结构(第五章)

蓝Q曦 included in 数据结构

2024-04-09 2210 words 5 minutes

Contents

数组和广义表

数组的定义

数组是我们很熟悉的一种数据结构，它可以看作线性表的推广。数组作为一种数据结构其特点是结构中的元素本身可以是具有某种结构的数据，但属于同一数据类型，比如：一维数组可以看作一个线性表，二维数组可以看作“数据元素是一维数组”的一维数组，三维数组可以看作“数据元素是二维数组”的一维数组，依此类推

数组的顺序表示

由于数组中各元素具有统一的类型，并且数组元素的下标一般具有固定的上界和下界，因此，数组的处理比其它复杂的结构更为简单。多维数组是一维数组的推广
例如，二维数组A
二维数组A可以看成是由m个行向量组成的向量，也可以看成是n个列向量组成的向量
数组一旦被定义，它的维数和维界就不再改变。因此，除了结构的初始化和销毁之外，数组只有存取元素和修改元素值的操作
由于计算机的内存结构是一维的，因此用一维内存来表示多维数组，就必须按某种次序将数组元素排成一列序列，然后将这个线性序列存放在存储器中
数组一旦建立，结构中的元素个数和元素间的关系就不再发生变化。因此，一般采用顺序存储的方法来表示数组
行优先顺序或以行为主序存储方式：将数组元素按行排列，第i+1个行向量紧接在第i个行向量后面。以二维数组为例，按行优先顺序存储的线性序列为：

$a_{11},a_{12},…,a_{1n},a_{21},a_{22},…a_{2n},……,a_{m1},a_{m2},…,a_{mn}$
在PASCAL、C等语言中，数组就是按行优先顺序存储的。
**$LOC(a_{ij})=LOC(a_{11})+[(i-1)n+j-1]d$
列优先顺序或以列为主序存储方式：将数组元素按列向量排列，第j+1个列向量紧接在第j个列向量之后，A的m*n个元素按列优先顺序存储的线性序列为

$a_{11},a_{21},…,a_{m1},a_{12},a_{22},…a_{m2},……,a_{n1},a_{n2},…,a_{nm}$
在FORTRAN语言中，数组按列优先顺序存储
$LOC(a_{ij})=LOC(a_{11})+[(j-1)*m+i-1]*d$
行优先顺序——先排最右的下标，从右到左，最后排最左下标
列优先顺序——先排最左下标，从左向右，最后排最右下标
例如：三维数组Amnp以行优先方式顺序存储，则

$LOC(a_{ijk})=LOC(a_{111})+[(i-1)mn+ (j-1)*n+(k-1)]*d$

数组存储的特点

只要知道开始结点的存放地址（即基地址）、维数和每维的上、下界，以及每个数组元素所占用的单元数，就可以将数组元素的存放地址表示为其下标的线性函数。因此，数组中的任一元素可以在相同的时间内存取，即顺序存储的数组是一个随机存取结构

矩阵的压缩存储

压缩存储：为多个值相同的非零元素只分配一个存储空间；对零元素不分配空间

特殊矩阵的压缩存储

特殊矩阵：非零元素按照一定的规律分布
常见的特殊矩阵有对称矩阵、三角矩阵、对角矩阵等
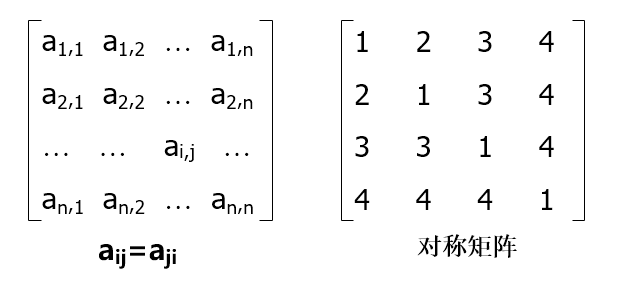
1. 对称矩阵：元素的值按照主对角线对称
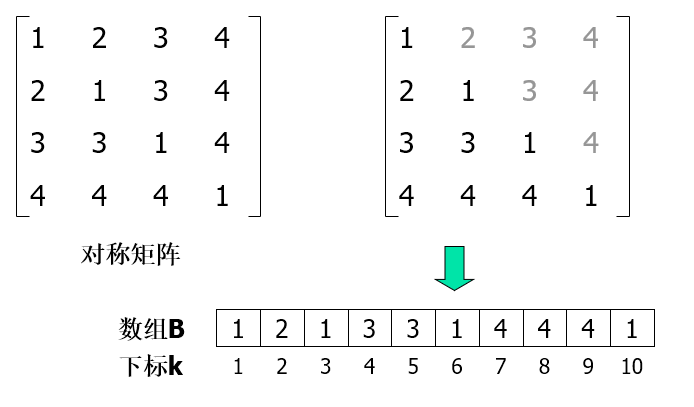
例如：一个4*4的对称矩阵
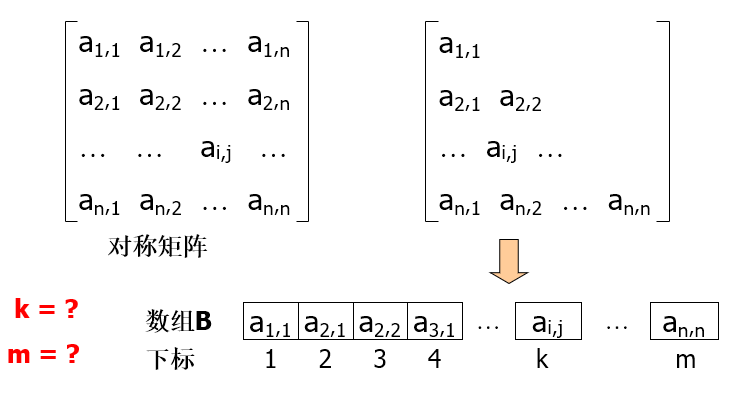
推广至一般情况，n*n的对称矩阵
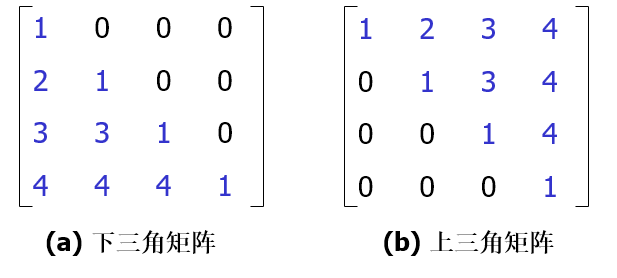
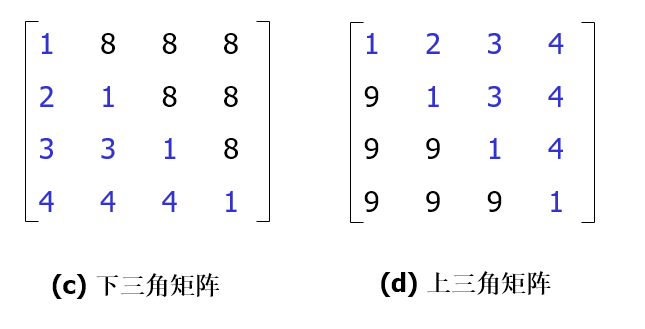
三角矩阵：上(下)三角矩阵是指矩阵的下（上）三角（不包括对角线）中的元素均为常数或零的n阶矩阵，即非零元素的分布在矩阵中呈现为三角形
例如：一个4*4的三角矩阵。
例如：一个4*4的三角矩阵
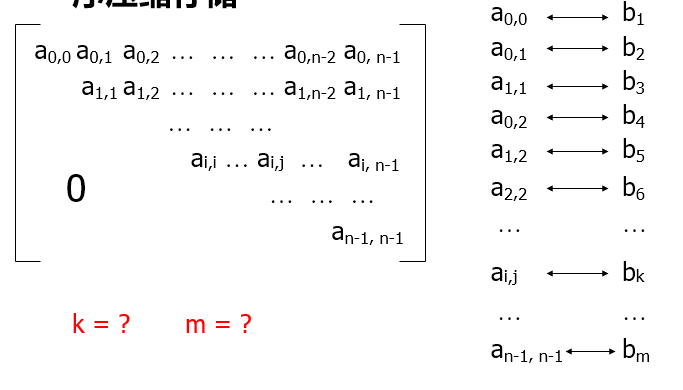
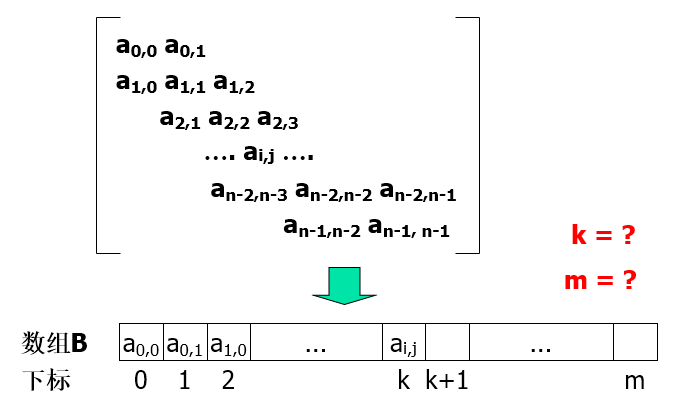
推广至一般情况，n*n的三角矩阵以行为主序压缩存储
对角矩阵是指所有的非零元素都集中在以主对角线为中心的带状区域中
上述各种特殊矩阵，其非零元素的分布都是有规律的，因此总能找到一种方法将它们压缩存储到一维数组中，并且一般都能找到矩阵中的元素与该一维数组元素的对应关系，通过这个关系，仍能对矩阵的元素进行随机存取

稀疏矩阵

什么是稀疏矩阵？简单说，设矩阵A中有s个非零元素，若s远远小于矩阵元素的总数（即s«m×n），则称A为稀疏矩阵
设在矩阵A中，有s个非零元素。令 e=s/(m*n)，称e为矩阵的稀疏因子。通常认为e≤0.05时称之为稀疏矩阵
在存储稀疏矩阵时，由于非零元素的分布一般是没有规律的，因此在存储非零元素的同时，还必须同时记下它所在的行和列的位置（i,j)。反之，一个**三元组(i,j,aij)**惟一确定了矩阵A的一个非零元。因此，稀疏矩阵可由表示非零元的三元组及其行列数唯一确定
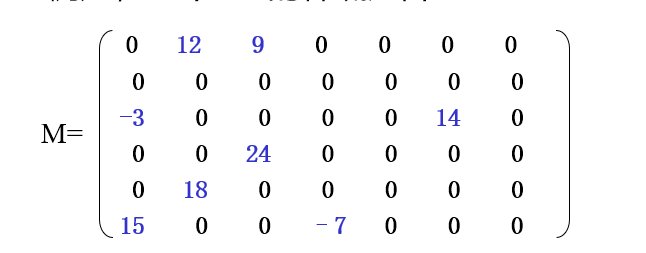
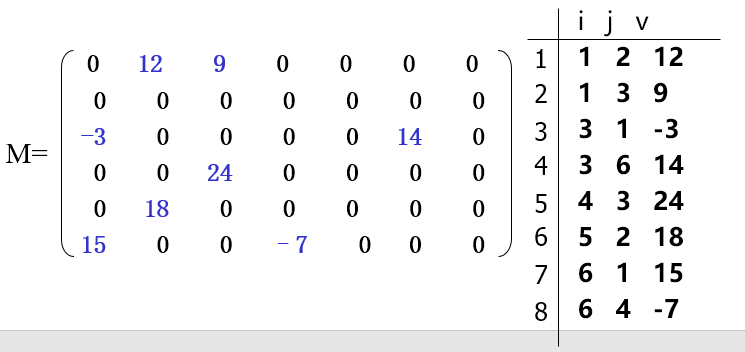
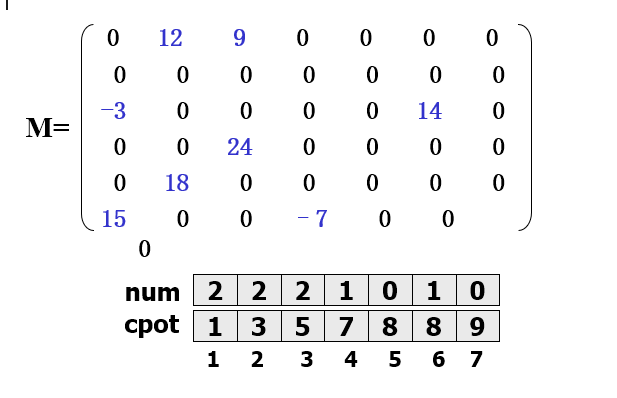
例如，一个6*7的稀疏矩阵
稀疏矩阵中的非零元素

( (1,2,12), (1,3,9), (3,1,-3), (3,6,14), (4,3,24), (5,2,18), (6,1,15), (6,4,-7) )

假设以顺序存储结构来表示三元组表，则可得到稀疏矩阵的一种压缩存储方法——三元组顺序表

#define maxsize 10000
typedef int datatype;
typedef struct{
    int   i,j;
    datatype v;
}triple;  /* 三元组*/
typedef struct{
    triple  data[maxsize];
    int  m,n,t;
}tripletable;

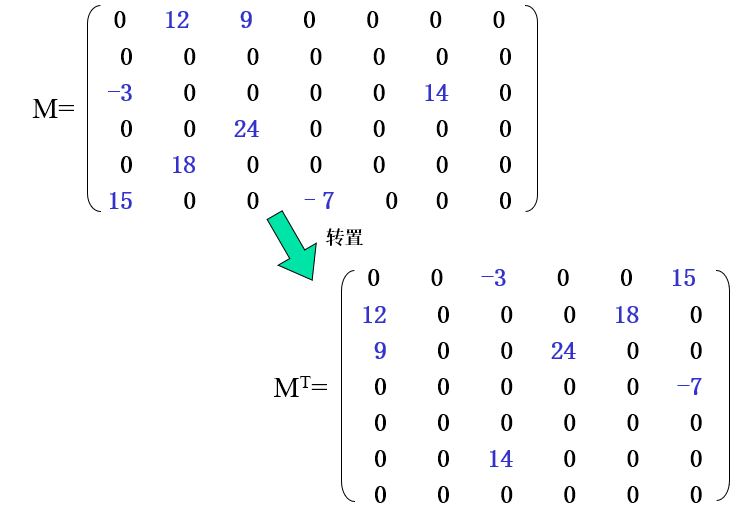
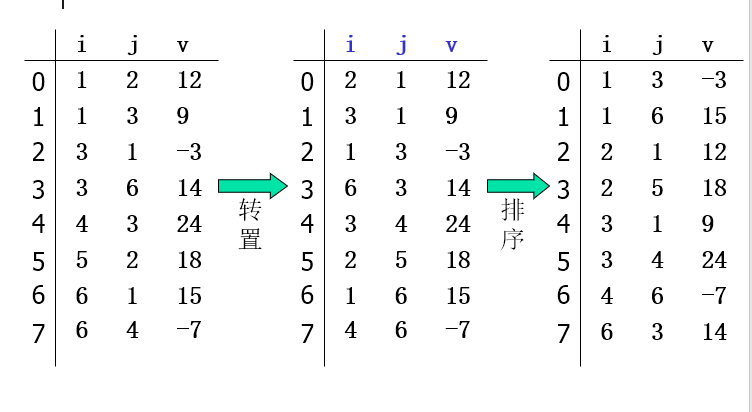
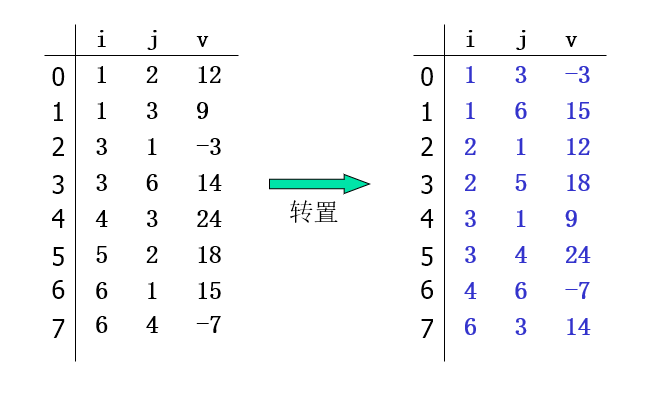
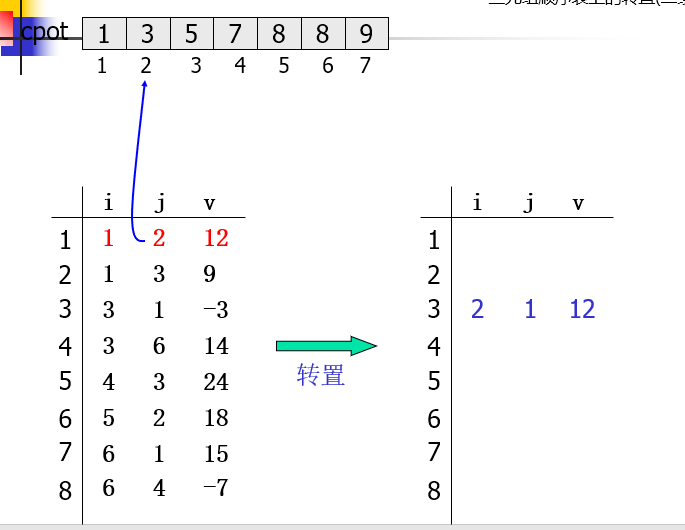
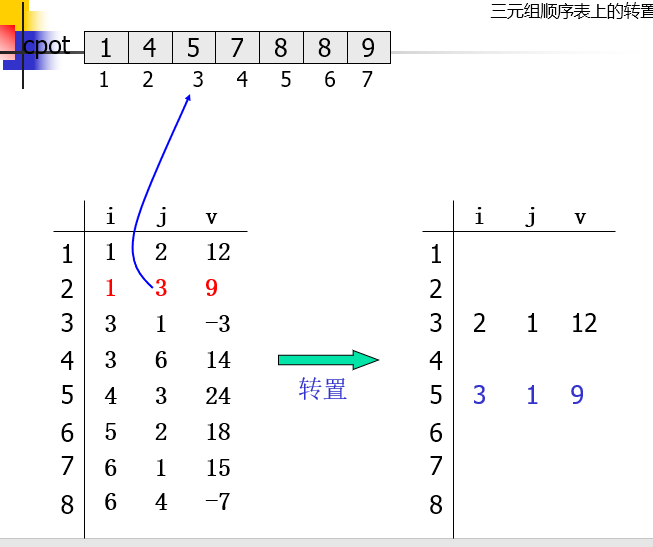
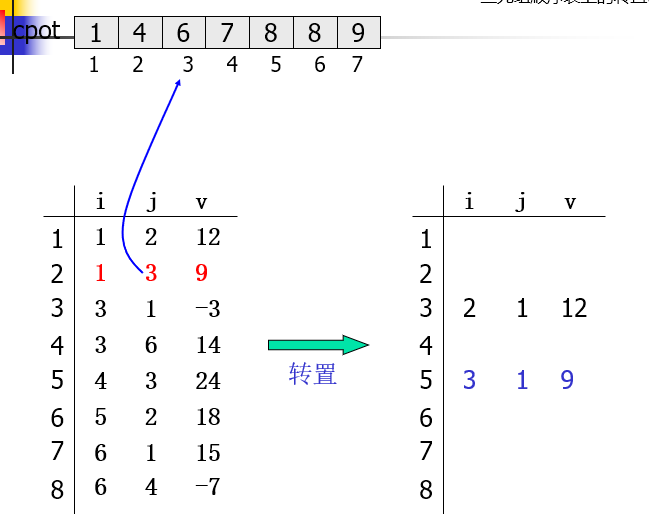
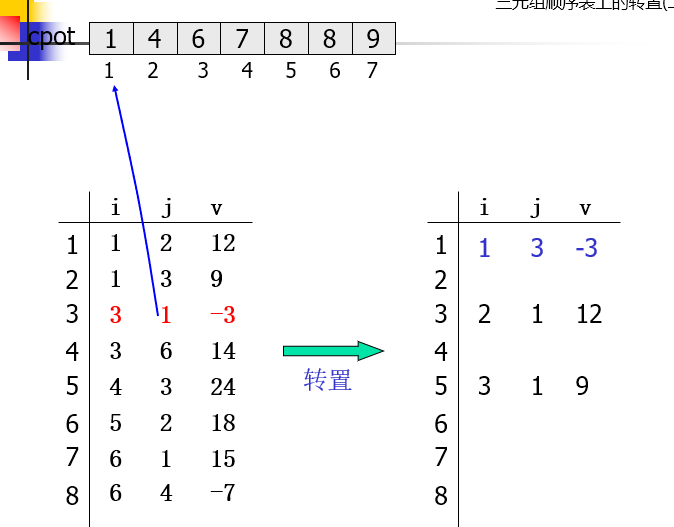
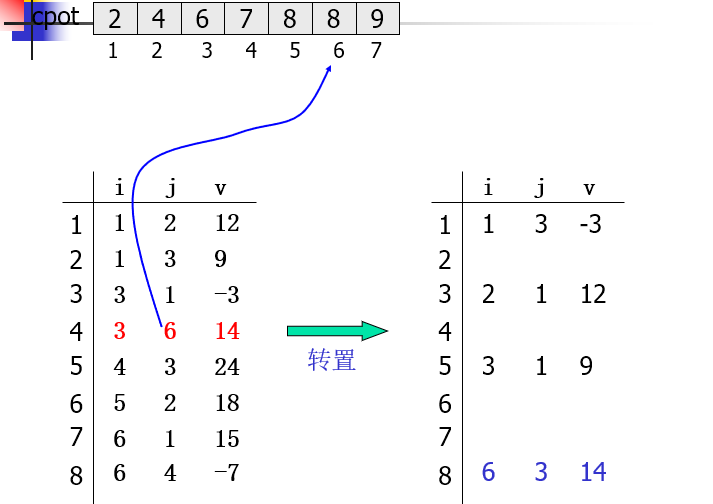
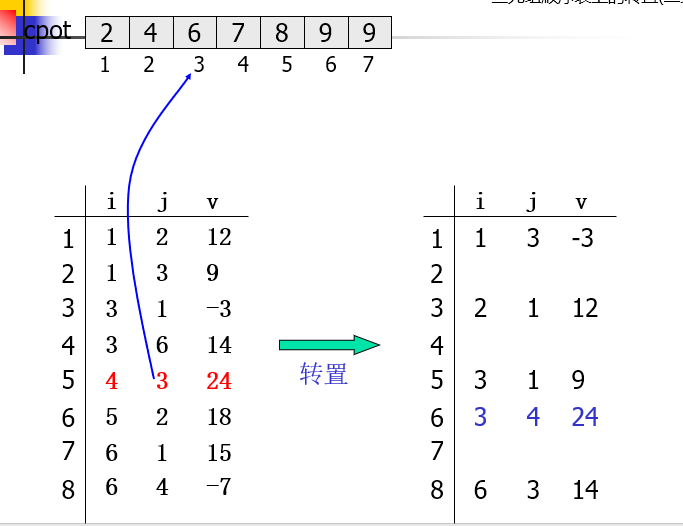
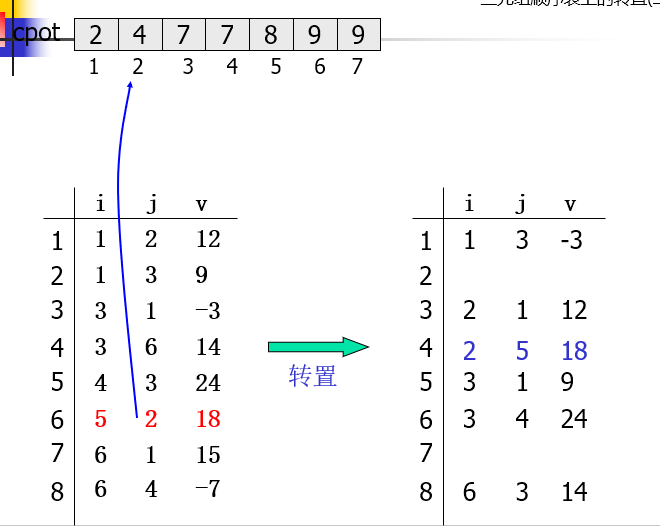
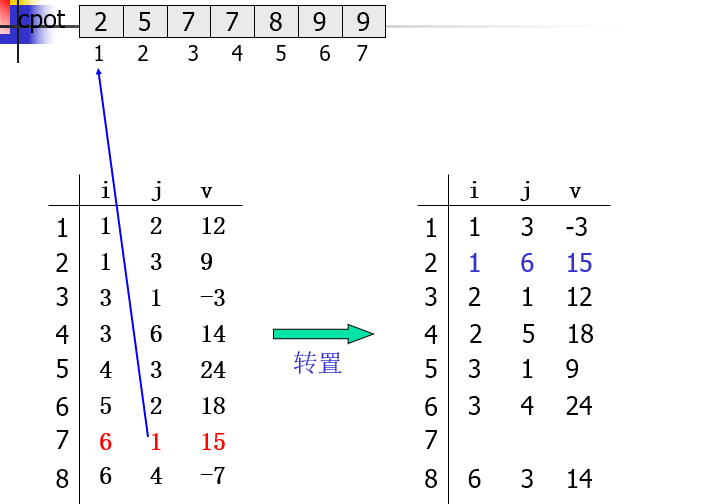
三元组顺序表上的转置

Void transmatrix(tripletable A,  tripletable  &AT)  { 
    AT.m=A.n;       AT.n=A.m;       AT.t=A.t; 
    if (AT.t<=0) return;
    for(p=0;p<A.t;++p)  {
          AT.data[p].i =  A.data[p].j;     AT.data[p].j =  A.data[p].i;
          AT.data[p].v =  A.data[p].v; 
      }
    //按照AT.data[p].i进行非递减排序
}

设置向量num,num[col]表示矩阵A中第col列中非零元的个数。(A的列数：A.n)

for(col=1;col<=A.n;++col)  num[col] = 0;

for(p=1;p<=A.t;++p)  //计算A中每列非零元的个数
       num[A.data[p].j]++;  //A.data[p].j为列号

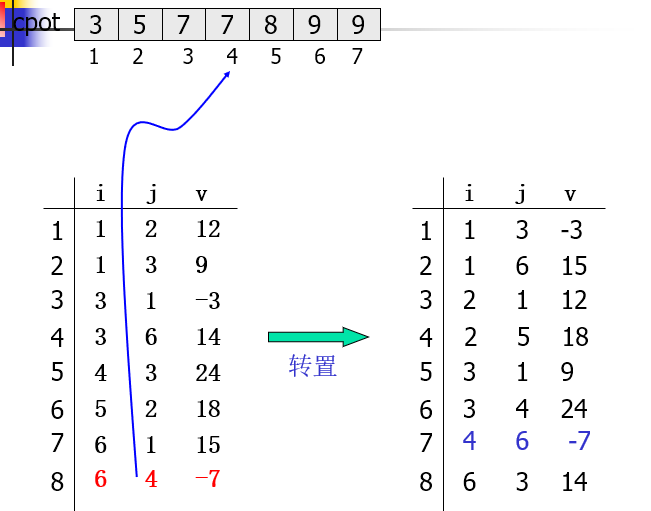
设置向量cpot,cpot[col]指示A中第col列的第一个非零元在转置矩阵AT.data中的恰当位置

cpot[1]=1;
for(col = 2; col<=A.n; ++col)
      cpot[col]=cpot[col-1]+num[col-1];

for(col=1;col<=A.n;++col)  num[col] = 0;
for(p=1;p<=A.t;++p)  //计算A中每列非零元的个数
       num[A.data[p].j]++;
cpot[1]=1;
for(col = 2; col<=A.n; ++col) //计算元素位置
      cpot[col]=cpot[col-1]+num[col-1];
for(p = 1; p<=A.t; ++p)  {//转置
     col = A.data[p].j;   q = cpot[col];
     AT.data[q].i = A.data[p].j; 
     AT.data[q].j = A.data[p].i; 
     AT.data[q].v = A.data[p].v;
     cpot[col]++;
}

广义表的定义

广义表是线性表的推广
1. $L=(a_1,a_2,…,a_n ),n≥0,a_i$可以是单元素，也可以是一个表
例如
1. A = ()
2. B = (e)
3. C = (a,(b,c,d))
4. D = (A,B,C)
5. E = (a,E)
广义表的长度
广义表的深度
非空广义表
1. 表头(Head)：第一个元素
2. 表尾(Tail)：除第一个元素外其余元素构成的表
链表存储
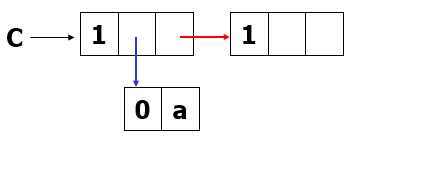
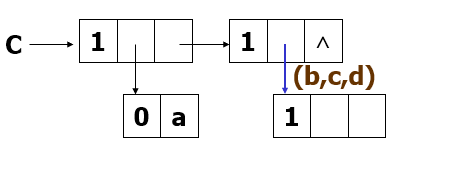
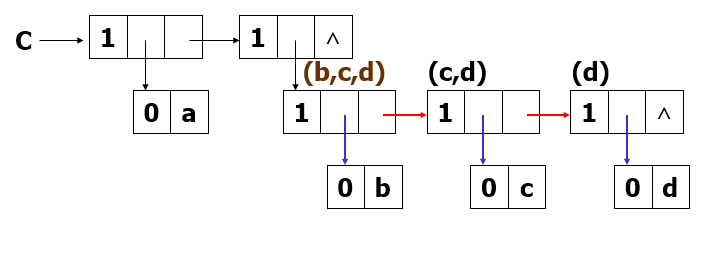
1. C = (a,(b,c,d))
2. D = (A,B,C)
3. E = (a,E)
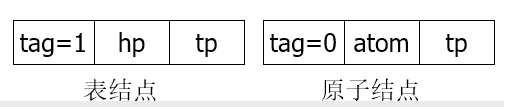
链表结点结构
C = (a,(b,c,d))
Head(C) = a Tail(C)=((b,c,d))
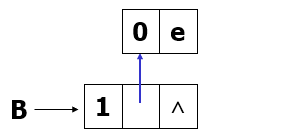
B= (e)
A= ()
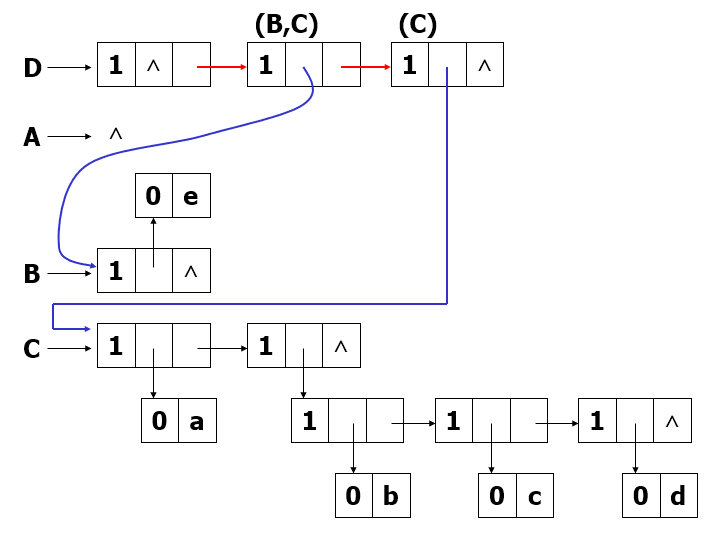
D= (A,B,C)

结点结构

typedef enum {ATOM,LIST} ElemTag;
typedef struct GLNode{
        ElemTag  tag;
        union {
             AtomType atom;
             struct GLNode *hp;
        };
        struct GLNode *tp;
}*Glist;

m元多项式的表示

本章小结

本章应掌握的内容
1. 数组的按行存储和按列存储
2. 特殊矩阵的压缩存储
3. 广义表的定义、基本运算(求表头、表尾)
4. 广义表的存储结构