串

串的定义及基本运算

1. 串的定义

   串(String)是零个或多个字符组成的有限序列。一般记作：S=“a1a2a3…an”，其中：

   S：串名；

   “a1a2a3…an”：串值，双引号括起来的字符序列；

   ai(1≤i≤n)可以是字母、数字或其它字符；

2. 串的长度

   串中所包含的字符个数；

   长度为零的串称为空串(Empty String)，它不包含任何字符

3. 空白串

   通常将仅由一个或多个空格组成的串称为空白串(Blank String)。

   注意：空串和空白串的不同。

4. 串的子串

   串中任意个连续字符组成的子序列称为该串的子串(SubString)，包含子串的串相应地称为主串。通常将子串在主串中首次出现时的该子串的首字符对应的主串中的序号，定义为子串在主串中的序号（或位置）。

   1. 例如：设A和B分别为A=“This is a string” B=“is”

      则B是A的子串，A为主串。B在A中出现了两次，其中首次出现所对应的主串位置是3。因此，称B在A中的位置为3。

   特别地，空串是任意串的子串，任意串是其自身的子串。

5. 串的基本运算

   1. 串赋值: StrAssign(&S, char *t)
   2. 串比较: int StrCompare(S, T)
   3. 求串长: int StrLength(S)
   4. 串联接: char *strcat(char *to, char *from)
   5. 求子串: SubString(&sub, S, pos, len)
   6. 串复制 : char *strcpy(char *to,char *from)
   7. 子串定位: int index(Sub,S)

串的表示和实现

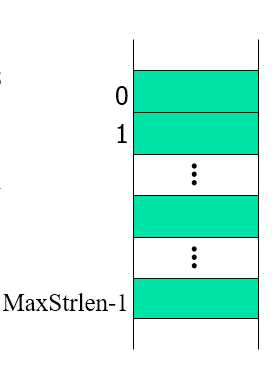
1. 串的定长顺序存储

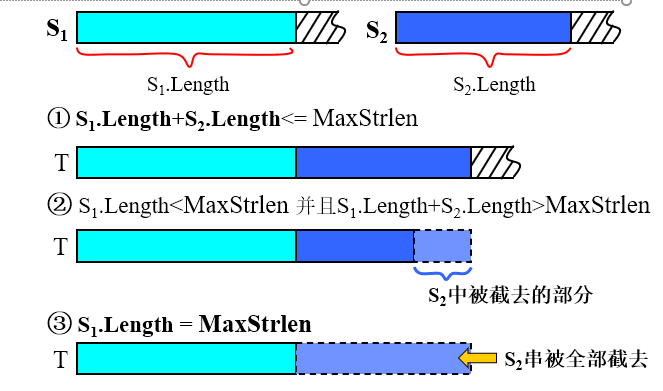
   #define maxstrlen 256
   typedef char sstring[maxstrlen];
   sstring s;   //s可容纳255个字符
   

   串作为高级语言支持的数据类型，对于串长度(或串的结尾表示)，会有不同的方式，对于超过串存储空间的部分会截断存储。

   可以在串定义中加入串长表示

   typedef struct{
           char ch[MaxStrlen];
           int length;
   }sstring;
   

   

   1. 顺序串的操作实现

      1. 串连接Concat(&T,S1,S2)

         

      2. 求子串SubString(&Sub,S,pos,len)

         Status SubString(Sstring &Sub,Sstring S,int pos,int len){
         	     //求串S从第pos个字符起长度为len的子串Sub
         	     if (pos<1 || pos > S.Length || len<0 || len>S.Length-pos+1)
         	             return  ERROR;
         	     Sub.ch[0..len-1] = S.ch[pos-1..pos+len-2];
         	     Sub.length = len;
         	}
         

   2. 串的堆分配存储

      在程序执行过程中从内存空闲区(堆)中动态申请满足串长的存储空间，串在其中仍是顺序存储的，称为堆结构。也称为动态存储分配的顺序表。

      1. 串的堆分配存储定义

         ① typedef char *string;  //c中的串库相当于此类型定义
         		② //-----串的堆分配存储表示-----
           typedef struct{
                 char *ch;
                 int  length;
         　 }Hsring;
         

      2. 基本操作的实现

         1. 串赋值

            Status strassign(Hstring &T,char *chars){
             	  //生成一个其值等于串常量chars的串T
                  if(T.ch)  free(T.ch);
                  for(i = 0,c = chars;c; ++i,++c); //求chars长度
                  if(!i) { T.ch = null; T.length = 0; }
                  else{
                     if (!(T.ch = (char *)malloc(i*sizeof(char))))
                      	exit(OVERFLOW);
            		    T.ch[0..i-1] = chars[0..i-1];
            		    T.length = i;
                  }
            	   return  OK;
            }
            

         2. 串联接

            Status concat(Hstring  &t, Hstring s1, Hstring s2){ 
            //将串s1和s2联接成新串t
              if (!(t.ch) = (char*)malloc(s1.length+
                                                s2.length)*sizeof(char)))
                     exit(overflow);
              t.ch[0..s1.length-1] = s1.ch[0..s1.length-1];
              t.length = s1.length + s2.length;
              t.ch[s1.length..t.length-1] = s2.ch[0..s2.length-1];
            return  OK;
            }
            

         3. 求子串

             Status substr(Hstring &sub,Hstring s,int pos,int len){
            	    if (pos<1 || pos>s.length || len<0 || 
                                         len>s.length-pos+1)
            		       return error;
                   if (sub.ch)  
                        free(sub.ch);
                   if (!len) { sub.ch = null; sub.length = 0; }
             	    else{
            		      sub.ch = (char *)malloc(len*sizeof(char));
            		      sub.ch[0..len - 1] = s[pos-1..pos + len-2];
            		      s.length = len;
                    }
            }
            

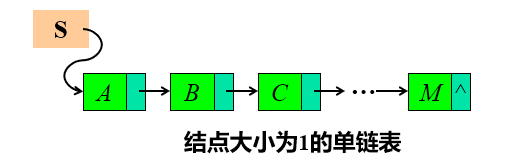
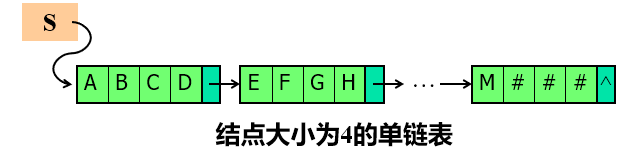
   3. 串的链式存储

      

      存储密度：

      $\frac{串值所占的存储空间}{实际分配的存储空间}$

      

串的模式匹配

子串定位运算又称为模式匹配(Pattern Matching)或串匹配(String Matching)。

在串匹配中，一般将主串称为目标串，子串称为模式串。

若子串在主串中出现，则称匹配成功，子串出现的位置称为有效位移,否则称匹配不成功。

模式匹配在文章的关键字查找中被广泛使用

1. 模式匹配算法

   1. 朴素的串匹配算法

      【数据结构】串（二）—— 朴素模式匹配算法-CSDN博客

      int Index(sstring S,sstring T,int pos) {
      //返回子串T在主串S中从第pos个字符开始的位置
      //要求T非空，1≤pos ≤Strlength(S)
        i = pos;  j = 1;
        while (i <= Strlength(S) && j <= Strlength(T)) {
              if (S[i]==T[j]) {++i; ++j;}
              else {i = i-j+2;  j = 1;}
        }
        if ( j> Strlength(T) )  return  (i–Strlength(T));
        return 0;
      } // Index
      

      算法时间复杂度

      O(n*m)，其中n、m分别为主串和子串长度

   2. 改进的串匹配算法－－KMP算法

      int Index_KMP(sstring S,sstring T,int pos) {
      //返回子串T在主串S中从第pos个字符开始的位置
      //要求T非空，1≤pos ≤Strlength(S)
        i=pos;  j=1;
        while(i<=Strlength(S) && j<=Strlength(T)) {
              if (               S[i]==T[j]) {++i; ++j;}
              else {i = i-j+2;  j = 1;} 
        }
        if (j> Strlength(T))  return  (i-Strlength(T));
        	    return 0;
      } // Index
      

      

      

      求next[j] 的算法：

      int Get_Index(sstring T, int next[]) {
      //求模式串T的next函数值并存入数组next
        i=1;  next[1]=0;  j=0;
        while(i<=Strlength(T)) {
              if ( j==0 || T[i]==T[j]) {++i; ++j;next[i]=j;}
              else  j=next[j]; 
        }
      } // Get_Index