数据结构(第三章)
栈和队列
栈
栈的定义及基本运算
-
栈(Stack)的定义
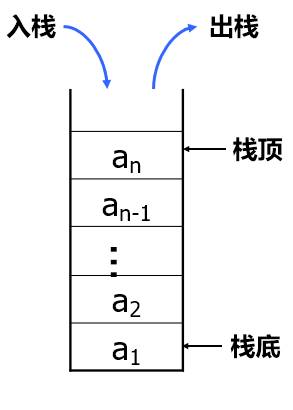
栈(Stack)是限制在表的一端进行插入和删除运算的线性表,通常称插入、删除的这一端为栈顶(top),另一端为栈底(bottom)。当表中没有元素时称为空栈。
-
栈的特点
栈的修改是按后进先出的原则进行的。因此,栈称为后进先出表(LIFO)。

-
栈的运算演示
- A、B、C、D四个元素依次进入一个栈,再依次出栈,得到一个输出序列DCBA。
-
栈的基本运算
- InitStack(&S): 初始化栈S
- StackEmpty(): 判断栈是否为空
- Push(e): 将元素e放入栈顶
- Pop(e): 移走栈顶的元素,同时由e带回该元素的值
- Gettop(): 获取栈顶的元素,但不从栈中移走
栈的存储结构和实现
-
栈的表示和实现
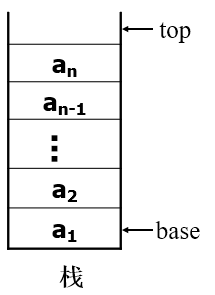
假设栈$S=(a_1,a_2,a_3,…,a_n)$,则**$a_1$称为栈底元素,$a_n$为栈顶元素**。栈中元素按$a_1,a_2,a_3,…,a_n$的次序进栈,退栈的第一个元素应为栈顶元素。换句话说,栈的修改是按后进先出的原则进行的。因此,**栈称为后进先出表(Last In First Out,LIFO) **

-
顺序栈
由于栈是运算受限的线性表,因此线性表的存储结构对栈也适应。栈的顺序存储结构简称为顺序栈,它是运算受限的线性表。因此,可用数组来实现顺序栈。
-
顺序栈的类型定义
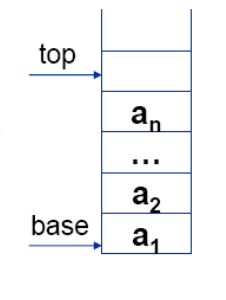
// -----栈的顺序存储表示----- # define STACK_INIT_SIZE 100; # define STACKINCREMENT 10; typedef struct { SElemType *base; //栈底指针,栈构造前和销毁后为空 SElemType *top; //栈顶指针,指向栈顶元素的下一位置 int stacksize; //当前分配的栈的存储空间数 }SqStack; -
顺序栈运算
设S是SqStack类型的指针变量。base是栈底指针。Top是栈顶指针。
- 栈不存在条件S.base=NULL
- 栈空条件S.top=S.base
- 插入栈顶元素,栈顶指针S.top=S.top+1
- 删除栈顶元素,栈顶指针S.top=S.top-1
- 栈满条件S.top-S.base>=S.stacksize

-
顺序栈的C语言实现
//初始化 Status InitStack(SqStack &S){ //构造一个空栈 S.base = (ElemType *) malloc(STACK_INIT_SIZE *sizeof(SElemType)) ; if(!S.base) exit (OVERFLOW); S.top = S.base; S.stacksize = STACK_INIT_SIZE ; return OK; }//InitStack //判断栈空 int StackEmpty(SqStack &S) { return(S.base==S.top); } //判断栈满 int StackFull(SqStack &S) { return(S.top-S.base>=S.stacksize); } //元素入栈 Status Push(SqStack &S, SElemType e){ //插入元素e为新的栈顶元素 if (S.top – S.base >= S.stacksize) return OVERFLOW; //栈满 *S.top = e; S.top++; return OK; }//Push //出栈 void Pop(SqStack &S, SElemType &e) { if(S.top==s.base) return UNDERFLOW; // 栈空 S.top--; e=*S.top; return; } -
链栈
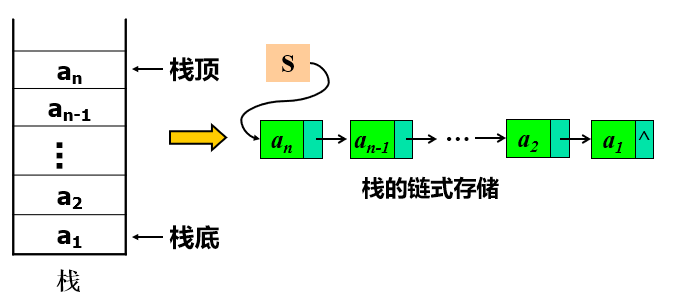
栈的链式存储结构称为链栈,它是运算是受限的单链表,插入和删除操作仅限制在表头位置上进行。由于只能在链表头部进行操作,故链表没有必要像单链表那样附加头结点。栈顶指针就是链表的头指针。
//链栈的类型说明如下: typedef struct stacknode { SElemType data; struct stacknode *next; } stacknode,*linkstack;
-
链栈的基本操作
//置空栈 void InitStack(linkStack &p) { p=NULL; } //判断栈空 int StackEmpty(linkstack p) { return p==NULL; } //进栈 void Push(linkstack &p, SElemType e) { stacknode *q; q=(stacknode*)malloc(sizeof(stacknode)); q–>data=e; q–>next=p; p=q; //设置栈顶指针 } //退栈 SElemType Pop(linkstack &p) { SElemType x; //临时变量,保存栈顶元素 linkstack q=p; if(p==NULL) error(“stack underflow.”); p=p–>next; //调整栈顶指针 x=q–>data; free(q); //删除栈顶元素 return x; } //取栈顶元素 SElemType GetTop(linkstack p) { if(p==NULL) error(“stack is empty.”); return p–>data; }
栈的应用举例
根据栈的FILO特性,用作某些处理问题的工具。
数制转换
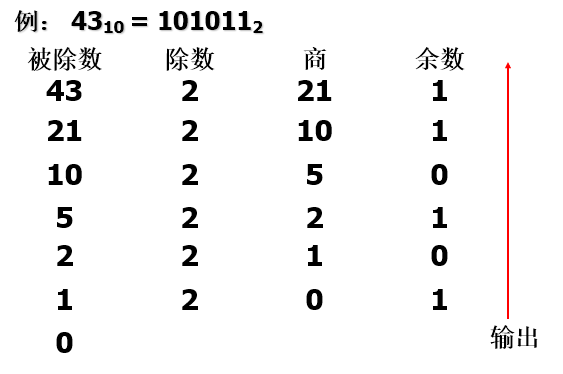
void conversion( ) {
InitStack(S); //构造空栈
scanf (“%d”,&n);
while(n){
Push(S,n%2);
n=n/2;
}
while(! StackEmpty(S)){
Pop(S,e);
printf(“%d”,e);
}
}
括号匹配
设一个表达式中可以包含三种括号:“(”和“)”、“[”和“]”、“{”和“}”,并且这三种括号可以按照任意的次序嵌套使用,考查表达式中的括号是否匹配。例如: …[…{…[…}…]…]…[…]…(…)…)…
例:
a=b+(c-d)*(e-f));
while (m<(a[8]+t)
{
m=m+1; t=t-1;
}
实现方法--利用栈进行表达式中的括号匹配
自左至右扫描表达式,若遇左括号,则将左括号入栈,若遇右括号,则将其与栈顶的左括号进行匹配,若配对,则栈顶的左括号出栈,否则出现括号不匹配错误。
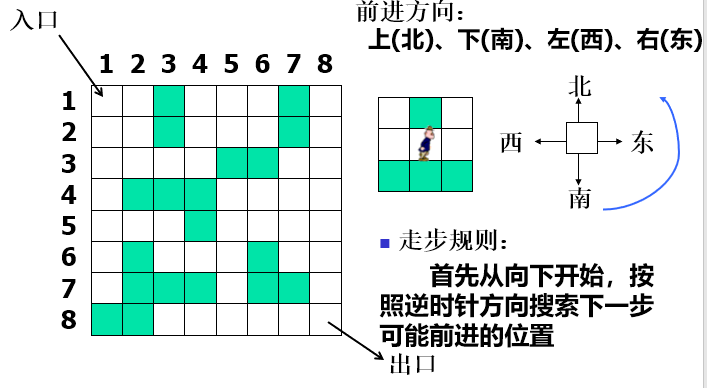
迷宫问题
寻找一条从入口到出口的通路
-
迷宫的表示
const int N=8; struct PosType{ int x, y; }; char maze[N][N]; //位置上的标识,是否可通过 -
迷宫初始化
用二层嵌套循环对迷宫赋值
-
迷宫求解
#define _CRT_SECURE_NO_WARNINGS 1 #include <stdio.h> #include <stdlib.h> #define STACK_INIT_SIZE 100 //存储空间初始分配量 #define STACKINCREMENT 10 //存储空间分配增量 #define MAXLENGTH 25 //迷宫最大行列值 #define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 typedef struct { int x; int y; }PosType; //坐标 typedef struct { int ord; //通道块在路径上的序号 PosType seat; //通道块在迷宫中的坐标 int di; //从此通道块走行下一通道块的方向 }SElemType; //栈元素类型 typedef struct Stack{ SElemType* base; //栈底指针 SElemType* top; //栈顶指针 int stacksize; //当前已分配的存储空间 }SqStack; typedef int Status; typedef int MazeType[MAXLENGTH][MAXLENGTH]; //声明全局变量 int x, y; //迷宫的行列数 int curstep = 1; //足迹路线,开始在入口处,每找到一个足迹递增1 PosType begin; //迷宫入口坐标 PosType end; //迷宫出口坐标 PosType direc[4] = { {0,1},{1,0},{0,-1},{-1,0} }; //移动方向依次位东南西北 MazeType maze; //迷宫数组(等价于maze[MAXLENGTH][MAXLENGTH]),此时未初始化值全为0 Status InitStack(SqStack* S); Status StackEmpty(SqStack S); Status Push(SqStack* S, SElemType e); Status Pop(SqStack* S, SElemType* e); Status ClearStack(SqStack* S); Status DestroyStack(SqStack* S); void Init(); void Print(); void MarkPrint(PosType e); Status Pass(PosType b); void FootPrint(PosType b); PosType NextPos(PosType b, int di); Status MazePath(PosType start, PosType end); int main() { Init(); //初始化迷宫 if (MazePath(begin, end)) { printf("此迷宫的一条路径如下\n"); Print(); } else { Print(); printf("没有通道\n"); } return 0; } //栈的基本操作部分 Status InitStack(SqStack* S) { //申请一个动态数组,为栈创建存储空间 S->base = (SElemType*)malloc(STACK_INIT_SIZE*sizeof(SElemType)); if (!S->base) exit(EXIT_FAILURE); S->top = S->base; //此时栈顶指针和栈底指针相同 S->stacksize = STACK_INIT_SIZE; return OK; } Status StackEmpty(SqStack S) { if (S.base == S.top) return TRUE; else return FALSE; } Status Push(SqStack* S, SElemType e) { if (S->top - S->base >= S->stacksize) { S->base = (SElemType*)realloc(S->base, (S->stacksize + STACKINCREMENT) * sizeof(SElemType)); if (!S->base) exit(EXIT_FAILURE); S->top = S->base + S->stacksize; S->stacksize += STACKINCREMENT; } *S->top++ = e; //等同*S->top == e; S->top++; return OK; } Status Pop(SqStack* S, SElemType* e) { if (!S->base) return ERROR; else if (S->base == S->top) return ERROR; --(S->top); *e = *(S->top); return OK; } Status ClearStack(SqStack* S) { S->base = S->top; return OK; } Status DestroyStack(SqStack* S) { S->top = NULL; S->stacksize = 0; free(S->base); return OK; } //迷宫实现部分 void Init() { int i, j; int x1, y1; printf("请输入迷宫的行列数:\n"); scanf("%d %d", &x, &y); //赋值时将最外面一圈设置为墙,所以x-1 y-1 for (i = 1; i < x - 1; i++) for (j = 1; j < y - 1; j++) maze[i][j] = 1; printf("请设置迷宫内有几个墙:\n"); scanf("%d", &j); printf("请输入迷宫内每个墙的位置:\n"); for (i = 0; i < j; i++) { scanf("%d %d", &x1, &y1); maze[x1][y1] = 0; } printf("迷宫结构如图\n"); Print(); printf("请输入入口的行列数\n"); scanf("%d %d", &begin.x, &begin.y); printf("请输入出口的行列数\n"); scanf("%d %d", &end.x, &end.y); } void Print() { int i, j; for (i = 0; i < x; i++) { for (j = 0; j < y; j++) printf("%3d", maze[i][j]); puts(""); } } void MarkPrint(PosType e) { maze[e.x][e.y] = -1; } Status Pass(PosType b) { if (maze[b.x][b.y] == 1) return OK; else return ERROR; } void FootPrint(PosType b) { maze[b.x][b.y] = curstep; } PosType NextPos(PosType b, int di) { b.x += direc[di].x; b.y += direc[di].y; return b; } //书上有参数MazeType maze,我们声明了全局变量所以不需要此参数 Status MazePath(PosType start, PosType end) { SqStack S; PosType curpos; SElemType e; InitStack(&S); curpos = start; //入口位置 //书上有curpos = 1,我们声明了全局变量所以不用此代码 do { if (Pass(curpos))//当前位置可以通过,未曾走到过的通道快 { FootPrint(curpos); //在此位置留下足迹 e.ord = curstep; e.seat = curpos; //位置 e.di = 0; //direc[0]是东所以先让e.di =0 Push(&S, e); if (curpos.x == end.x && curpos.y == end.y) return TRUE; curpos = NextPos(curpos, e.di); //下一位置是当前元素的东邻 curstep++; //探索下一步 } else { if (!StackEmpty(S)) { Pop(&S, &e); //退栈到前一位置,改变前一位置中的方向 curstep--; while (e.di == 3 && !StackEmpty(S)) //前一位置处于最后一个方向 { //此循环将栈中元素退回到还有被方向没有使用的坐标处 MarkPrint(e.seat); //留下不能通过的标记 Pop(&S, &e); //退回1步 curstep--; //足迹减1 } if (e.di < 3) { e.di++; //换下一个方向探索 Push(&S, e); //入栈该位置的下一方向 curstep++; curpos = NextPos(e.seat, e.di); } } } } while (!StackEmpty(S)); return FALSE; } -
输出栈中的路径
Status MazePath(maze, start, end) { //若迷宫中存在一条从入口start到出口end的通道,则求出这样的一条通路 InitStack(S); curpos = start; curstep = 1; do { if (pass(curpos)) { //当前位置可以通过 Mark(maze,curpos); //留下记号 e = (curstep,curpos,1); push(S,e); //加入路径 if (curpos==end) return true; //到达出口 curpos = NextPos(curpos,1) ;//下一个位置 curstep++; } else {//当前位置不能通过 if (!StackEmpty(S)){ pop(S,e); //退回一步 while(e.di==4 && ! StackEmpty(S)) {//当前位置是死胡同 Markdead(maze,e.seat);pop(S,e); //留下记号,沿来路返回 } if (e.di<4) { //当前位置还有其他方向没有探索,继续试探 e.di++; push(S,e); curpos =NextPos(e.seat, e.di); } } }while (!StackEmpty(S)); return false; }
表达式求值—算符优先法
4+2×3-10/5
– 先乘除,后加减;
– 从左算到右
– 先括号内,后括号外
– 4+2×3-10/5=4+6-10/5=10-10/5=10-2=8
- 表达式由操作数(operand)、运算符(operator)和界限符(delimiter)组成的。
- 将运算符和界限符统称为算符。它们构成的集合命名为OP
表达式求值
- 算符优先算法:用两个工作栈。一个称作OPTR,用于存放运算符;另一个称作OPND,用以存放操作数或运算结果。
- 首先置操作数栈为空栈,表达式起始符“#”为运算符的栈底元素;
- 依次读入表达式中每个字符,若是操作数则进OPND栈,若是运算符,则和OPTR栈的栈顶运算符比较优先权后作相应操作,直到整个表达式求值完毕(OPTR栈的栈顶元素和当前读入的字符均为“#”)
OperandType EvaluateExpression() {
InitStack(OPTR); Push(OPTR,’#’);
InitStack(OPND); c = getchar();
while(c != ‘#’||GetTop(OPTR)!=‘#’){
if(!In(c,OP)) {Push(OPND,c); c=getchar();}
else //不是运算符则进栈
switch(Precede(GetTop(OPTR),c)){
case ‘<’: //栈顶元素优先权低
Push(OPTR,c); c=getchar();
break;
case ‘=’: //脱括号并接收下一字符
Pop(OPTR,x); c=getchar();
break;
case ‘>’: //退栈并将运算结果入栈
Pop(OPTR,theta);
Pop(OPND,b); Pop(OPND,a);
Push(OPND,Operate(a,theta,b));
break;
} //switch
}//while
return GetTop(OPND);
}//EvaluateExpression
栈与递归的实现
用栈结构实现程序设计语言中函数的嵌套调用和递归调用
例:
long f(int n)
{
if (n>1) return n*f(n-1);
else return 1;
}
void main( )
{
int n=4;
printf(“%ld”,f(n));
}
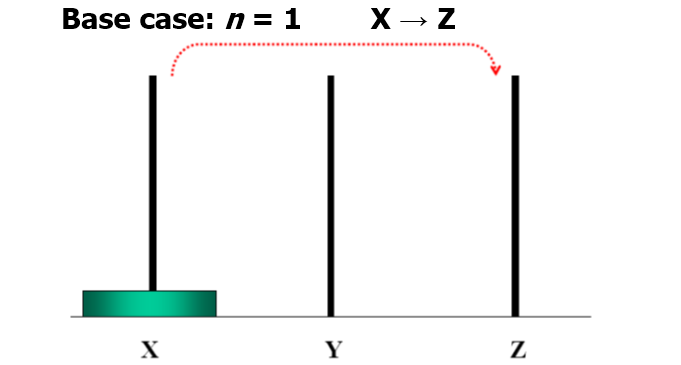
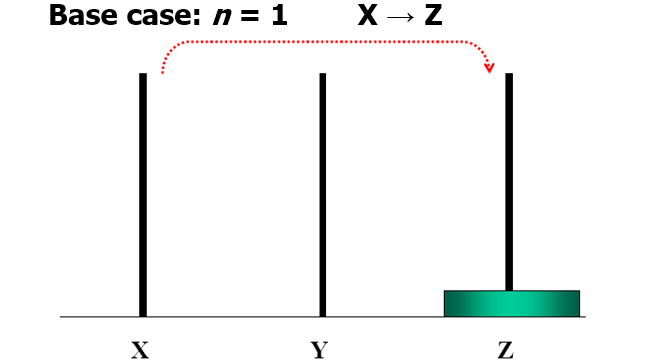
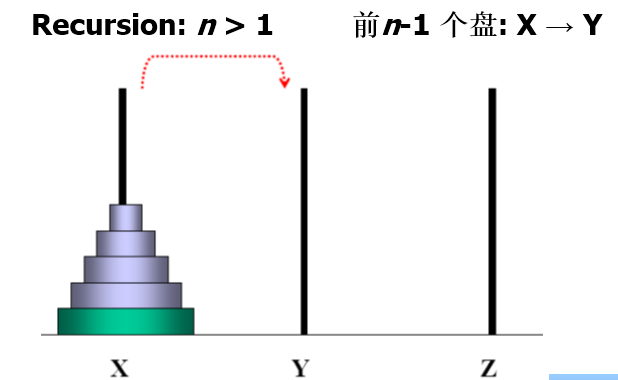
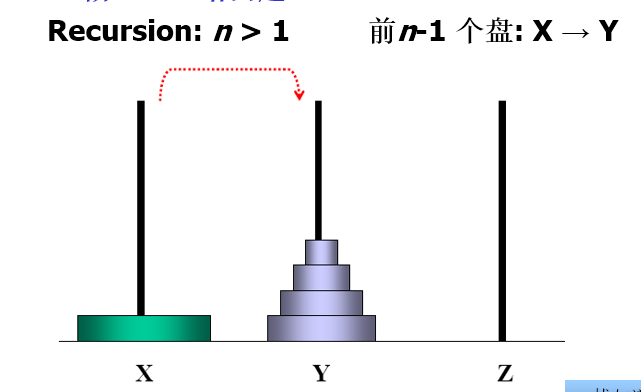
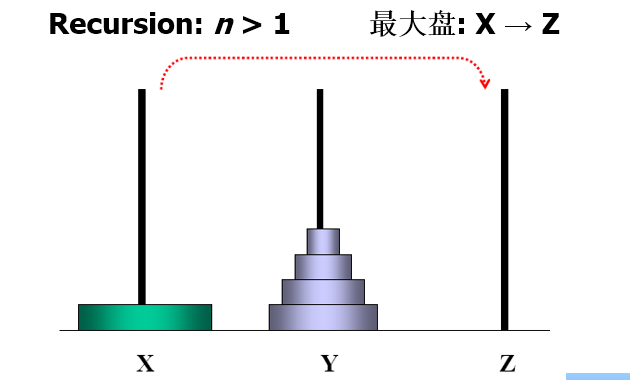
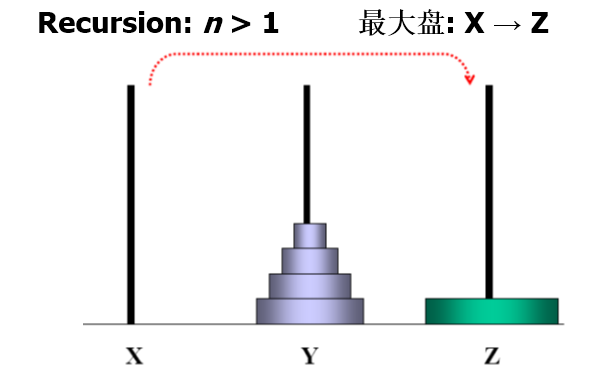
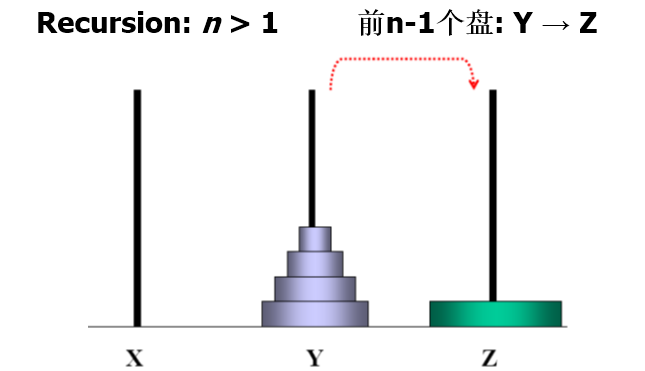
n阶Hanoi塔 问题
假设有三个分别命名为X、Y和Z的塔座,在塔座X上插有n个直径大小各不相同、依小到大编号为1,2,…,n的圆盘。现要求将X轴上的n个圆盘移至塔座Z上并仍按同样顺序叠排。
- 每次只能移动一个圆盘;
- 圆盘可以插在X、Y和Z中的任一塔座上
- 任何时刻都不能将一个较大的圆盘压在较小的圆盘之上。
队列(Queue)的定义
队列是仅限定在表尾进行插入和表头进行删除操作的线性表
- 术语
- 队头(front)--队列的表头,即只允许删除的一端。
- 队尾(rear) --队列的表尾,即只允许插入的一端。
- 入队(EnQueue) --向队尾插入元素
- 出队(DeQueue) --从队头删除元素

队列的特点
队列的修改是按先进先出的原则进行的。因此,队列称为先进先出表(FIFO)。
队列的基本运算
- InitQueue(&Q): 初始化队列Q
- QueueEmpty(): 判断队列是否为空
- EnQueue(e): 将元素e放入队尾
- DeQueue(e): 移走队头元素,由e带回该元素的值
- GetFront(): 获取队头元素的值,但不从队列中移走该元素
- Length(): 计算并返回队列中元素的个数
链队列--队列的链式存储结构
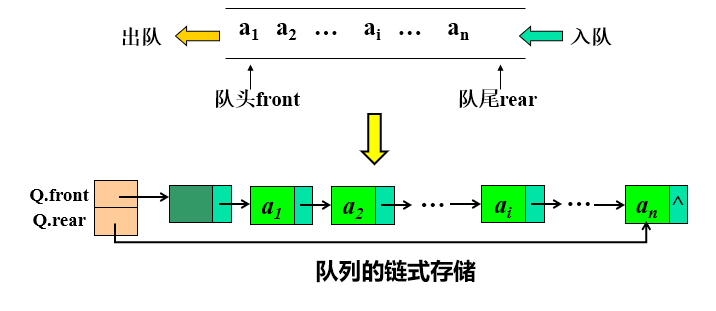
链队列的C语言实现
//-----单链队列的存储结构-----
typedef struct QNode{ //链表结点类型
QElemType data;
struct QNode *next;
}QNode,*QueuePtr;
typedef struct { //队列类型
QueuePtr front; //队头指针
QueuePtr rear; //队尾指针
}LinkQueue;
链队列基本操作的实现
-
初始化
Status InitQueue(LinkQueue &Q) { //构造一个空队列Q Q.front= Q.rear = (QueuePtr)malloc(sizeof(QNode)); if(!Q.front) exit(OVERFLOW); Q.front->next = NULL; return OK; } -
入队
Status EnQueue(LinkQueue &Q, QElemType e){ //将元素e插入到队列Q中 p = (QueuePtr)malloc(sizeof(QNode)); if (!p) exit(OVERFLOW); p->data = e; p->next=NULL; Q.rear->next = p; Q.rear = p; return OK; } -
出队列
Status DeQueue(LinkQueue &Q, QElemType &e){ //若队列不空,则队头元素出队列,用e返回其值, //返回OK,否则返回ERROR if (Q.rear == Q.front) return ERROR; p = Q.front -> next; e = p -> data; Q.front->next = p -> next; if (Q.rear == p) Q.rear = Q.front; free(p); return OK; }
循环队列--队列的顺序存储结构
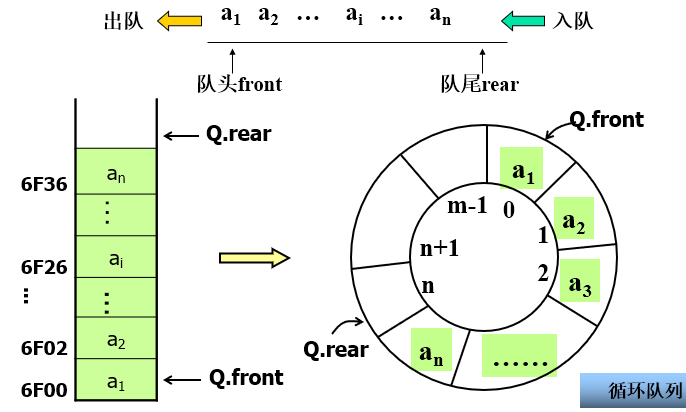
循环队列的C语言实现
//----循环队列的存储结构----
#define MAXSIZE 100
typedef struct {
QElemType *base;
int front;
int rear;
}SqQueue;
循环队列基本操作的实现
-
初始化
Status InitQueue(SqQueue &Q){ Q.base=(QElemType *) malloc(MAXSIZE*sizeof(QElemType)); if (!Q.base) exit (OVERFLOW); Q.front = Q.rear = 0; return OK; } -
入队
Status EnQueue(SqQueue &Q,QElemType e) { //将元素e插入队列Q的队尾 if ((Q.rear+1) % MAXSIZE == Q.front) return ERROR; Q.base[Q.rear] = e; Q.rear = (Q.rear+1) % MAXSIZE; return OK; } -
出队
Status DeQueue(SqQueue &Q,QElemType &e) { //删除队列Q的队头元素并用e带回 if (Q.front == Q.rear) return ERROR; e = Q.base[Q.front]; Q.front = (Q.front+1) % MAXSIZE; return OK; }
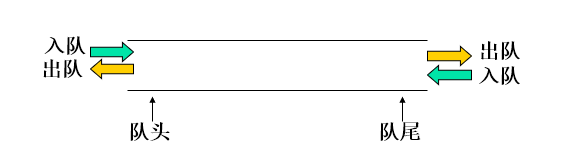
双端队列
-
双端队列

-
输出受限的双端队列

-
输入受限的双端队列

优先队列
- 在许多情况下,简单的队列结构是不够的,需要使用某些优先规则来完善先入先出机制
- 优先队列的问题是如何找到一种实现优先的方法,使得入队和出队列操作得以相对容易实现。
- 优先队列可以通过两种修正的链表结构来实现。
- 一种结构是元素仍然依次进入(即加入元素时,时间复杂度为O(1)),而取出元素时则需遍历队列(即出队时的时间复杂度为O(n)),
- 另一种是根据元素的优先级决定其插入的位置(即入队时的时间复杂度为O(n),出队时的时间复杂度为O(1))
队列的应用
同栈一样,队列也是一种应用广泛的线性表,在日常生活和计算机科学中很常见:
离散事件模拟
排队问题
作业控制
广度优先搜索
…