数据结构(第二章)
线性表定义
一个线性表是n个数据元素的有限序列
数据元素类型
- 原子型 整数,字符
- 结构类型 表示学生的数据元素
线性表中的元素之间的关系是线性关系
- 存在惟一的第一个元素
- 存在惟一的最后一个元素
- 除第一个元素之外,每个元素均只有一个直接前驱
- 除最后一个元素之外,每个元素均只有一个直接后继
顺序表
线性表的顺序存储
内涵
指用一组地址连续的存储单元依次存储线性表的数据元素。
特点
存储单元地址连续(需要一段连续空间)逻辑上相邻的数据元素其物理位置也相邻存储密度大(100%)
随机存取
元素序号与存储位置存在如下关系:
*Loc(ai) = Loc(ai)+(i-1)d (1<=i<=n)
线性表的动态分配顺序存储结构

在上述定义中,数组指针elem指示线性表的基地址,length指示线性表的当前长度。顺序表的初始化操作就是为顺序表分配一个预定义大小的数组空间,并将线性表的当前长度设为“0”.listsize指示顺序表当前分配的存储空间大小,一旦因插入元素而空间不足时,可再进行分配,即为顺序表增加一个大小为存储LISTINCREMENT个数据元素的空间

线性表上的基本运算
插入运算
含义
将元素e插入到线性表:($a_1,a_2,……,a_{i-1},a_i,……,a_n$)中,构成新的线性表($a_1,a_2,……,a_{i-1},e,a_i,……,a_n$),满足$a_{i-1}\leq e \leq a_i$,(其中$\leq$为比较关系),即不破坏原线性关系。
一般情况下,在第i($1\leq i \leq n$)个元素之前插入一个元素时,需将第n至第i(共n-1+1)个元素向后移动一个位置。
算法如下:
Status ListInsert Sq(SqList &L,int i ,ElemType e){
//在顺序线性表L中第i个位置之前插入新的元素额,
//i的合法值为1<=i<=ListLength_Sq(L)+1
if(i<1||i>L.length+1)
return ERROR; //i值不合法
if(L.length>=L.listsize){ //当前存储空间已满,增加分配
newbase = (ElemType *)realloc(L.elem,(L.listsize+LISTINCREMENT)*sizeof(ElemType));
if(!newbase)
exit(OVERFLOW); //存储分配失败
L.elem = newbase; //新基址
L.listsize+=LISTINCREMENT; //增加存储容量
}
q=&(L.elem[i-1]); //q为插入位置
for(p=&(L.elem[L.length-1]);p>=q;--p)
*(p+1)=*p; //插入位置及之后的元素右移
*q=e; //插入e
++L.length; //表长增1
return OK;
} //ListInsert_Sq
顺序表上插入运算效率分析
时间复杂度
最好情况:在表尾插入,不移动元素,T(n)=O(1)
最坏情况:在表头插入,移动n个元素,T(n)=O(n)
平均复杂度
设$p_i$为在第i个元素之前插入一个元素的概率,且$P_1=P_2=…=P_i=…P_n=1/(n+1)$,则平均移动次数为:
$E_is = \sum \limits^{n+1}{i=1}P_i(n-i+1)=1/(n+1)\sum\limits^{n+1}{i=1}(n-i+1)=n/2$
即T(n)=O(n)
空间复杂度
不需要额外空间,S(n)=O(1).
删除运算
顺序表上删除运算的实现

一般情况下,删除第i($1\leq i \leq n$)个元素时需将从第i+1至第n(共n-i)个元素依次向前移动一个位置
算法如下:
Status ListDelete_Sq(SqList &L,int i,ElemType &e){
//在顺序线性表L中删除第i个元素,并用e返回其值
//i的合法值为1<=i<=ListLength_Sq(L)
if((i<1) || (i>L.length))
return ERROR //i值不合法
p=&(L.elem[i-1]); //p为删除元素的位置
e=*p; //被删除元素的值赋给e
q=L.elem+L.length-1; //表尾元素的位置
for(++p;p<=q;++p)
*(p-1) = *p; //被删除元素之后的元素左移
--L.length; //表长减1
return OK;
}//ListDelete_Sq
顺序表上删除运算效率分析
平均复杂度
假设$q_i$是删除第i个元素的概率,则在长度为n的线性表中删除一个元素时所需移动元素次数的期望值(平均次数)为
$E_dl=\sum\limits^n_{i=1}q_i(n-i)=1/n\sum\limits^n_{i=1}(n-1)=(n-1)/2$
即:T(n)=O(n)
空间复杂度
S(n)=O(1)
顺序表的优缺点
优点
- 不需要额外的存储空间来表示元素间的逻辑关系
- 可以随机地存取表中的任意一个元素
缺点
- 插入和删除元素时要移动大量的元素
- 必须事先进行空间分配,表的容量难以扩充(新算法已解决)
类语言书写的算法与C程序之间的差别
- 算法中除形式参数外,变量不做定义,在C程序中必须定义
- 算法中使用的元素类型(ElemType)没有定义,C程序中必须定义,常量OK,ERROR,OVERFLOW等在第一章统一定义
- 算法中的比较运算符(equal,less)未作定义,C程序中必须定义
- 必要的头文件(用作输入输出的stdio.h及内存申请的stdlib.h),在C程序中必需包含
线性表的链式表示和实现
线性表的链式存储思路
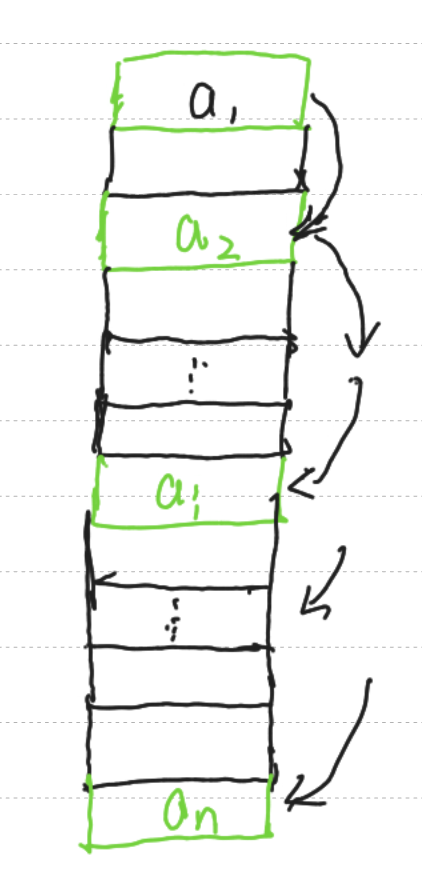
逻辑结构
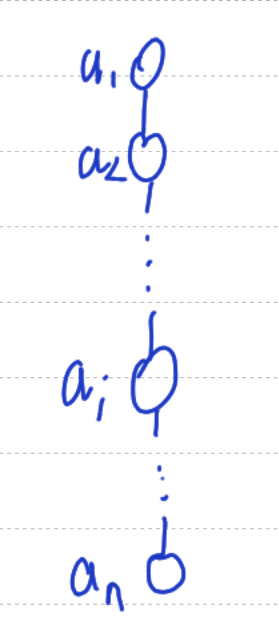
存储结构
实现方式
对每一个元素的存储单位进行扩充,在包含元素值存储的同时,在结点中存储与当前元素有直接关系的其他元素(直接前驱/直接后继)存储单位的地址(指针)
链式存储单位结构示意图
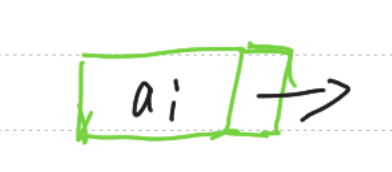
链表(线性表的链式存储)
内涵
线性表的链式存储指用任意的存储单位存放线性表中的元素,每个元素与其直接前驱和(或)直接后继之间的关系用指针来存储,这称为链表
术语
结点:数据元素及其有直接关系的元素的地址构成的存储单位
链表结点结构示意图
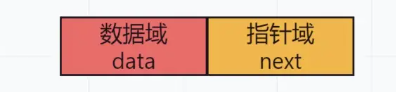

单链表
链表中,如果每个结点中只包含一个指针域,则称之为线性链表或单链表
单链表的存储
每个结点存储当前元素的直接后继。
线性表($a_1,a_2,…,a_{i-1},a_i,a_{i+1},…,a_n$)
链表示意图

单链表的内存镜像
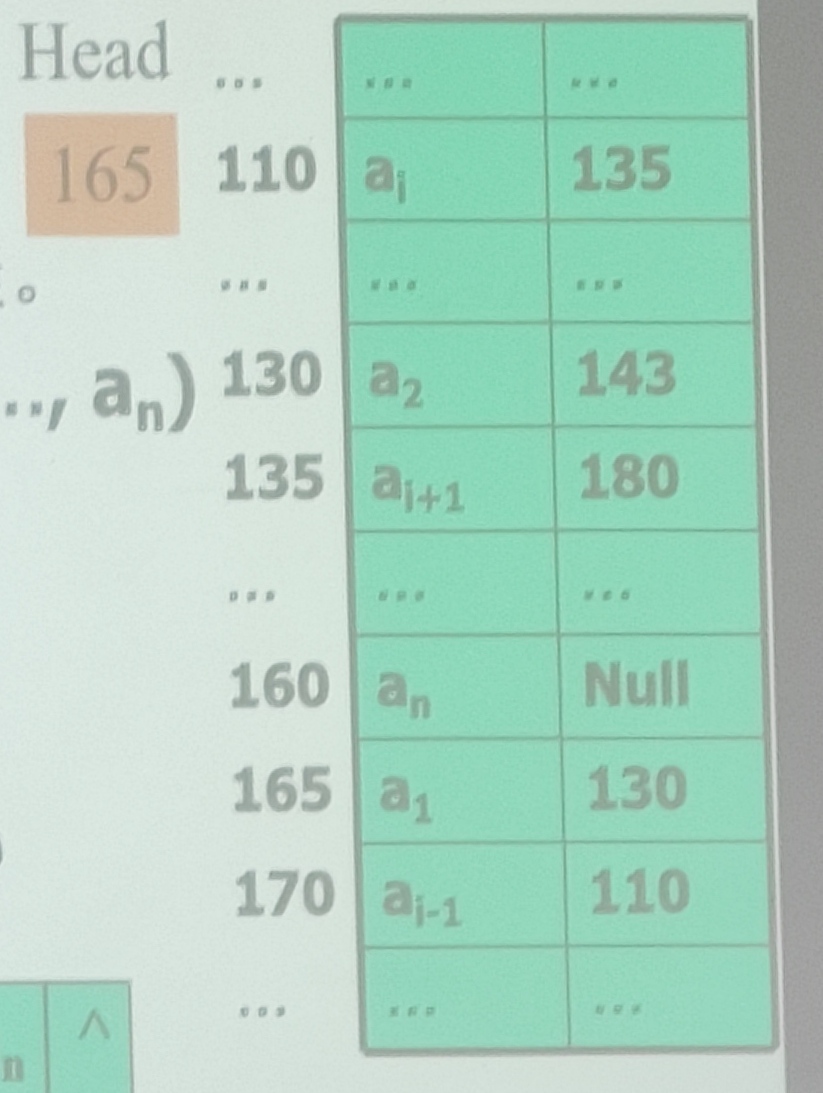
单链表的C语言实现
//用结构指针描述
typedef struct LNode{
ElemType data; //数据域
struct LNode *next //指针域
}LNode,*LinkList
与之对应的结点结构示意图
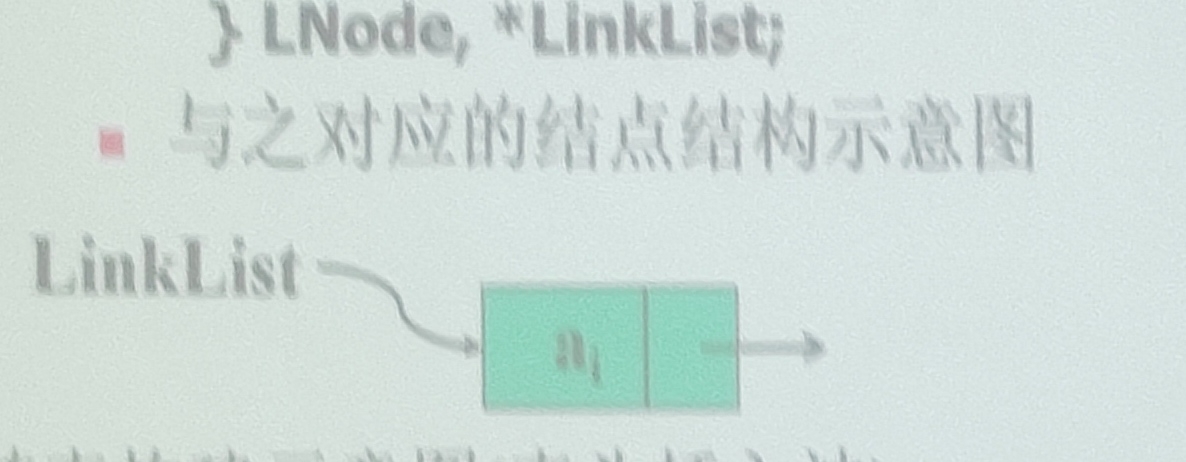
单链表构建示意图(表头插入法)
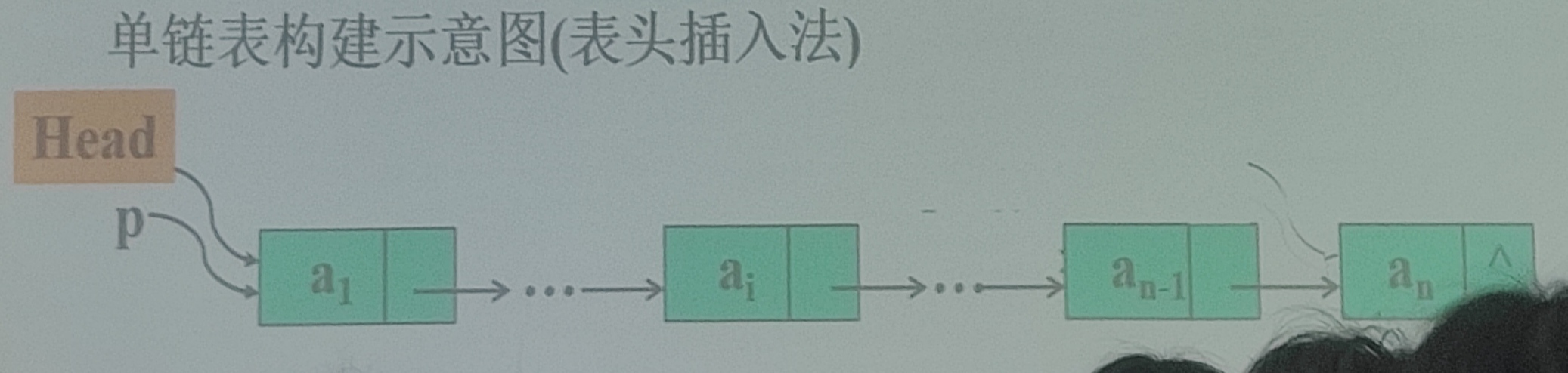
带头结点的单链表
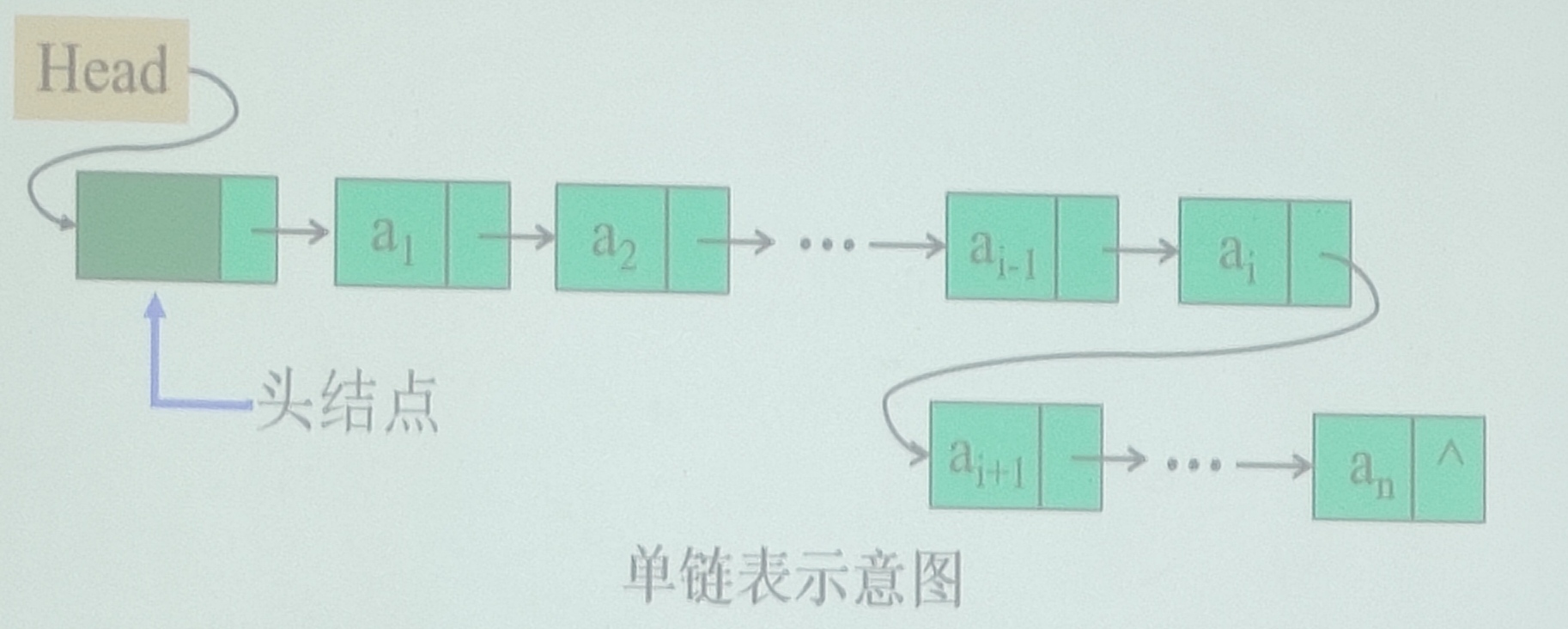
单链表上的查找运算
在单链表中,必须从头指针出发进行查找
-
查找第i个元素
-
查找指定元素是否在表中
-
…..
若找到,则返回该元素的值,否则返回ERROR
在单链表上查找第i个元素的示意图
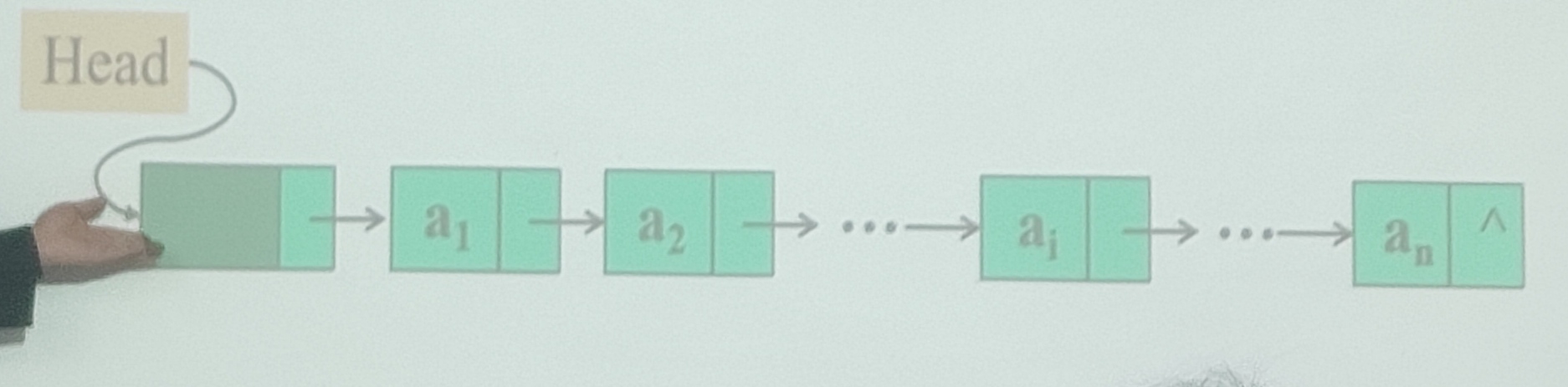
用类C语言实现单链表上的查询(查找第i个元素)
Status GetElem_L(LinkList L,int i,ElemType &e){
//L为带头结点的单链表的头指针
//当第i个元素存在时,其赋值给e并返回OK,否则返回ERROR
p=L->next;
j=1; //初始化,p指向第一个结点,否则返回ERROR
while(p&&j<1){
p=p->next;
++j;
}
if(!p||j>i)
return ERROR; //第i个元素不存在
e=p->data; //取第i个元素
return OK;
}//GetElem_L
单链表的插入运算(第i个位置插入新的结点)

用类C语言实现单链表上的插入(插入第i个元素)
Status ListInsert_L(LinkList &L,int i,ElemType e){
//在带头结点的单链线性表L中的第i个位置之前插入元素e
p=L;
j=0;
while(p&&j<i-1){
p=p->next;
++j;
} //寻找i-1个结点
if(!p||j>i-1)
return ERROR; //i小于1或者大于表长+1
s=(LinkList)malloc(sizeof(LNode)); //生成新结点
s->data=e;
s->next=p=>next; //插入L中
p->next=s;
return OK;
}//ListInsert_L
用类C语言实现单链表上的删除(删除第i个元素)
Status ListDelete_L(LinkList &L,int i,ElemType &e){
//在带头结点的单链线性表L中,删除第i个元素,并由e返回其值
p=L;
j=0;
while(p->next&&j<i-1){ //寻找第i个结点,并令p指向其前驱
p=p->next;
++j;
}
if(!(p->next)||j>i-1)
return ERROR; //删除位置不合理
q=p->next;
p->next=q->next; //删除并释放结点
e=q->data;
free(q);
return OK;
}//ListDelete_L
单链表的表示和实现
链表的优缺点
优点:
- 插入,删除时无需移动元素,只需修改指针
- 根据需要申请存储空间,且不要求连续的存储空间
缺点:
- 对表中的元素只能进行顺序访问
- 用指针指示元素之间的逻辑关系(直接前驱,后继),存储空间利用率低
用表头插入法建立结点的单链表
线性单链表存储结构
typedef struct LNode{
ElemType data;
struct LNode *next;
}LNode,*LinkList;

基本步骤
-
建立头结点:
L=(LinkList)malloc(sizeof(LNode)); L->next = NULL; -
建立新结点p,填入元素:
p = (LinkList)malloc(sizeof(LNode)); p->data=a; -
将新结点p插入到头结点之后,修改头结点指针域指向p:
p->next=L->next; L->next=p; -
重复2,3步骤直到插入所有结点,结束
用c语言实现表头插入算法
LinkList CreateList_LH(int n){
int i; //声明本函数的内部变量类型
LinkList head; //head为指向链表的指针类型
LNode *p //p为指向结点的指针类型
head=null;
for(i=n;i>0;--i){ //从后向前输入元素
p=(LNode *)malloc(sizeof(LNode)); //未做溢出判定,应加入
scanf("%d",&p->data); //将键盘输入置入p的数据域
p->next=head;
head=p; //返回指向链表的头指针
}
}
用表尾插入法建立带头结点的单链表
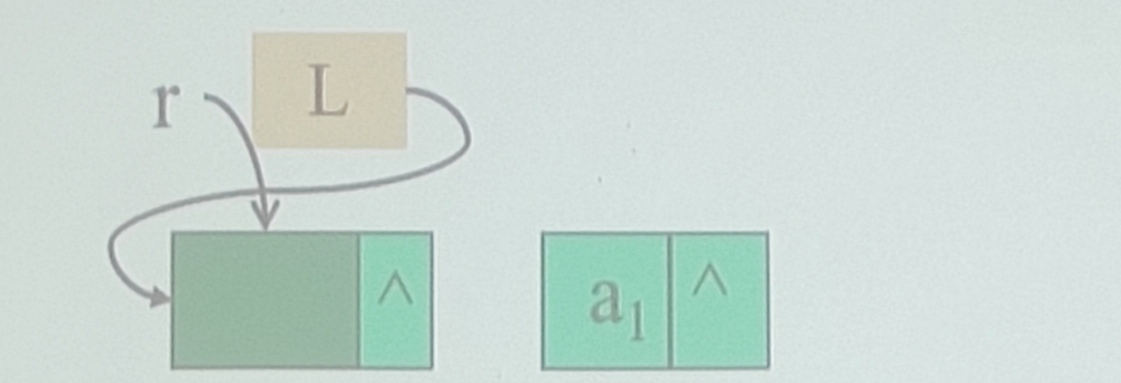
基本步骤
-
建立头结点,并附设一个指针r一直指向最后一个结点
L = (LinkList)malloc(sizeof(LNode)); L.next=NULL; r-L; -
申请一个新的结点空间,存入元素值
p=(LinkList)malloc(sizeof(LNode)); p->data=ai; p->next=NULL; -
将新结点插入链表尾部,r指向最后结点
r->next=p; r=p; -
重复2,3步骤直到最后一个结点,结束
用表尾插入法建立带头结点的单链表
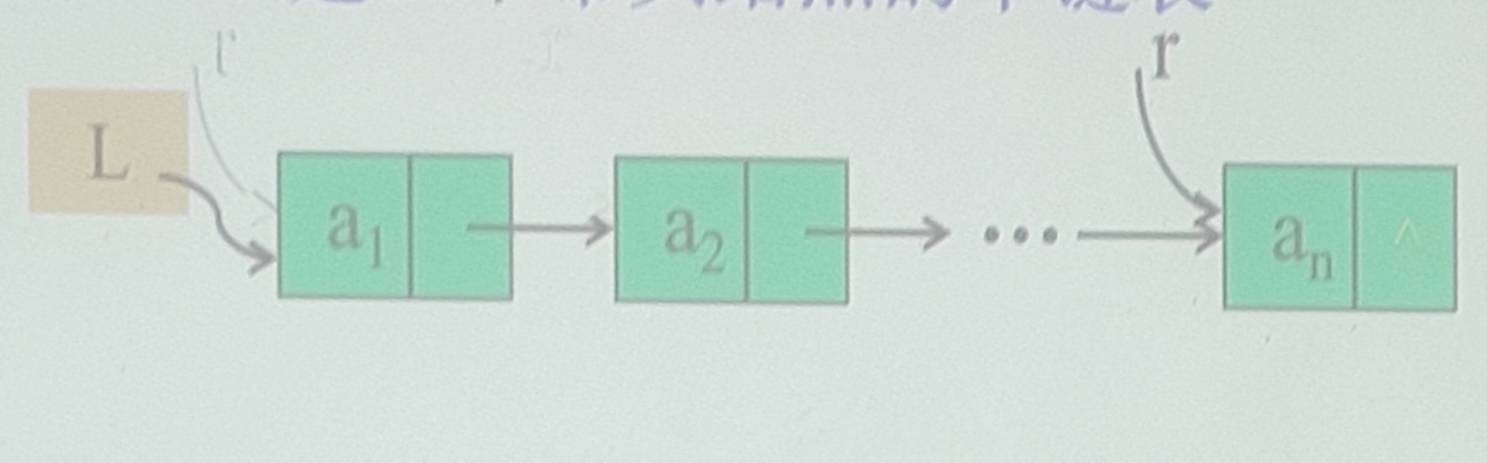
基本步骤
-
初始化指针Head和指向最后结点的指针r
head=NULL; r=NULL; -
申请一个新的结点并令p指向该结点,存入元素值
-
将新结点插入表尾
r->next=p; r=p; //注:表尾插入法建立的链表与输入元素顺序一致 //1.当r指向非空结点时使用上面的语句 //2.当r指向空地址时 head=p;r=p; -
重复2,3步骤直到最后一个结点,结束
用表尾插入法建立不带头结点的单链表(元素为字符,C语言)
LinkList CreateList_LT(){
char ch;
LinkList head;
LNode *p,*r; //p指向新申请的结点,r指向链表的尾结点
head=NULL;
r=NULL;
while((ch=getchar())!='\n'){
p=(LNode *)malloc(sizeof(LNode));
p->data=ch;
if(head==NULL) //插入第一个结点
head=p;
else
r->next=p; //插入第二个及以后的结点
r=p;
}
if(r!=NULL)
r->next=NULL;
return(head);
}
线性单链表删除
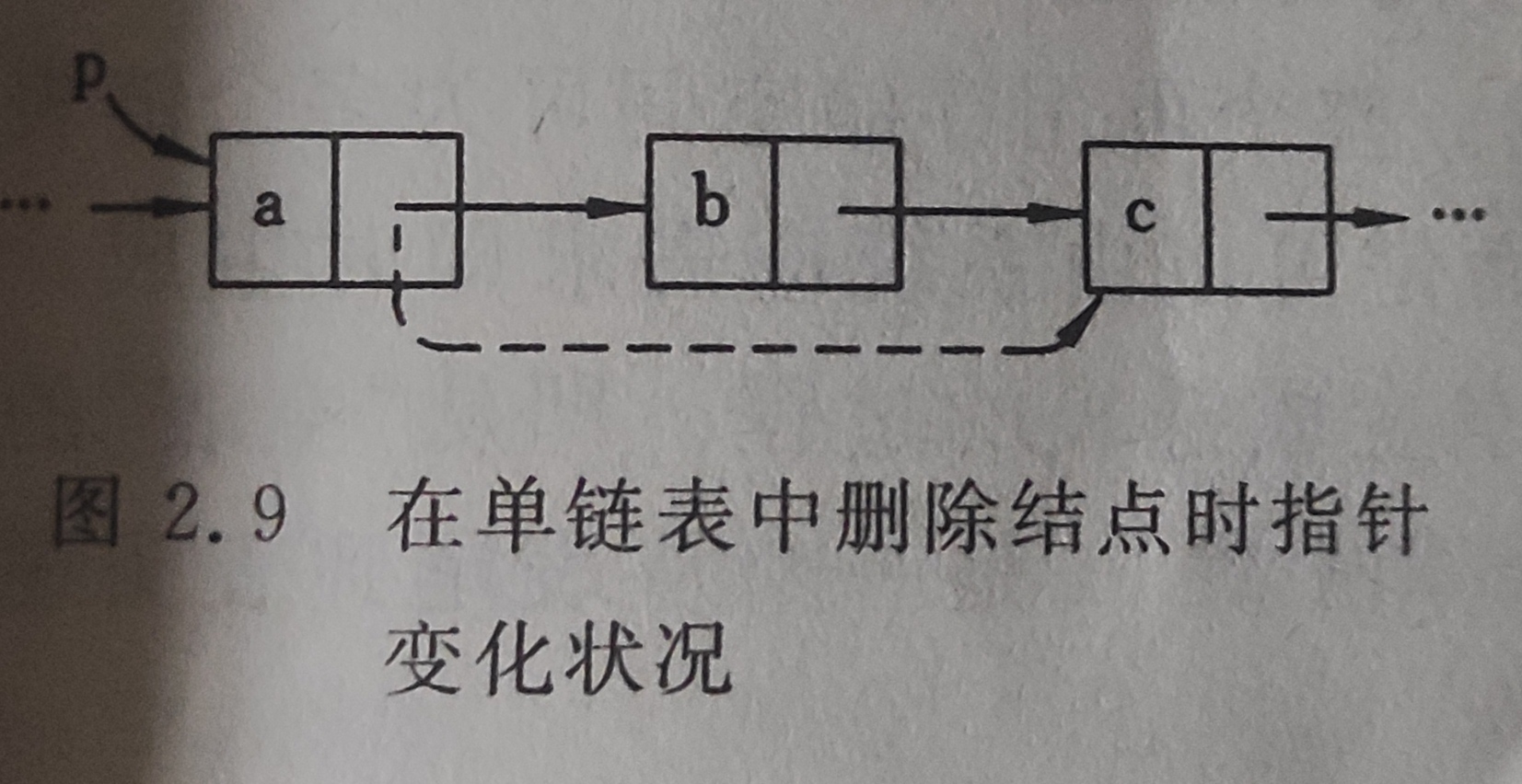
用类C语言实现线性单链表上的删除
Status ListDelete_L(LinkList &L,int i,ElemType &e){
//在带头结点的单链线性表L中,删除第i个元素,并由e返回其值
p=L;j=0;
while(p->next&&j<i-1){ 寻找第i个结点,并令p指向其前驱
p=p->next;
++j;
}
if(!(p->next)||j>i-1)
return ERROR; //删除位置不合理
q=p->next;
p->next=q->next; //删除并释放结点
e=q->data;
free(q);
return OK;
}//ListDelete_
循环单链表和双向链表
双向链表的插入操作(将元素e插入到链表的第i个结点前)
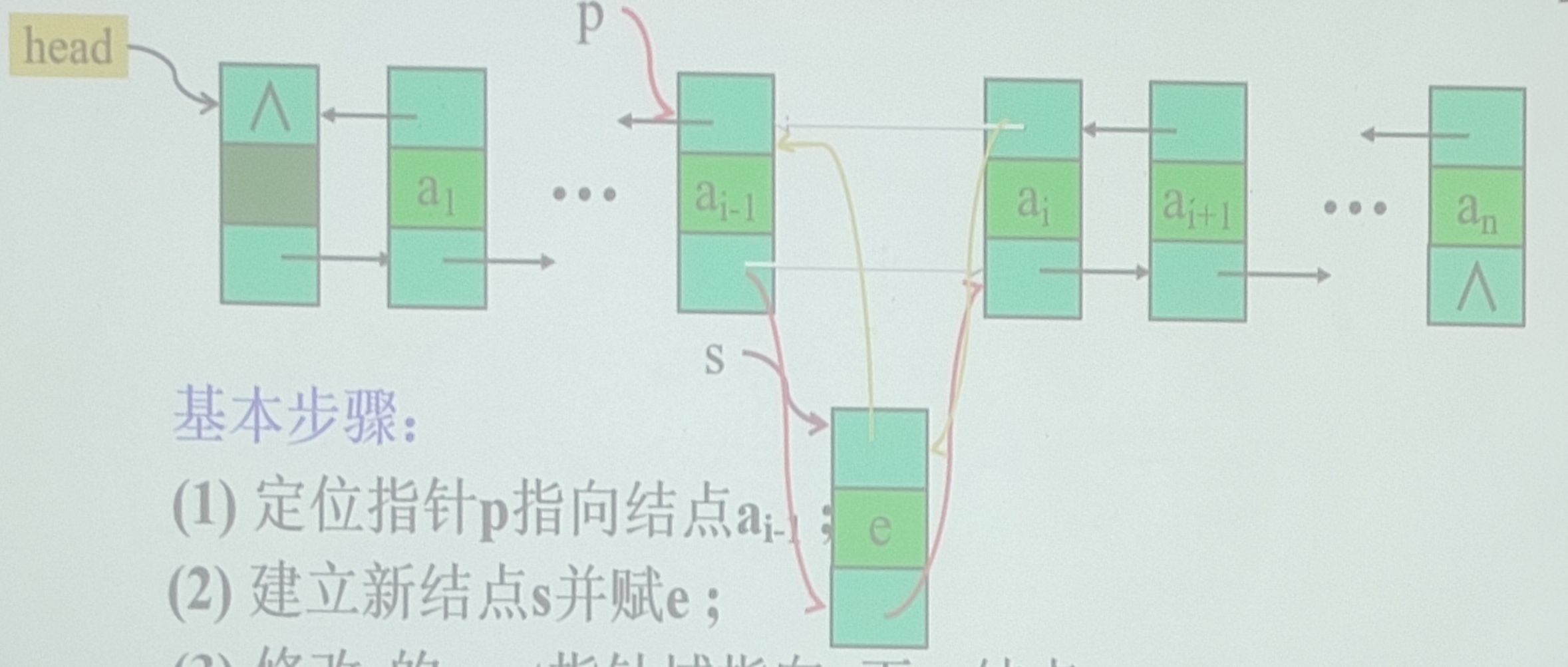
基本步骤
-
定位指针p指向结点$a_{i-1}$
-
建立新结点s并赋e;
-
修改s的next指针域指向p下一结点
s->next=p->next; -
修改s的prior指针域指向p结点
s->prior=p -
修改p的next指针域指向s结点
p->next=s -
修改s的下一结点的prior指针域指向s
s->next-prior=s
用类C语言实现双向循环链表插入
Status ListInsert_DuL(DuLinkList &L,int i,ElemType e){
//在带头结点的双链循环线性表L中第i个位置之前插入元素e
//i的合法值为1<=i<=表长+1
if(!(p=GetElemP_DuL(L,i))) //在L中确定插入位置指针p
return ERROR; //i等于表长加1时,p指向头结点;i大于表长加1时,p=NULL
if(!(s=(DuLinkList)malloc(sizeof(DuLNode))))
return ERROR;
s->data=e;
s->prior=p->prior;
p->prior->next=s;
s->next=p;
p->prior=s;
return OK;
}//ListInsert_DuL
双向链表的删除操作(删除第i个结点)
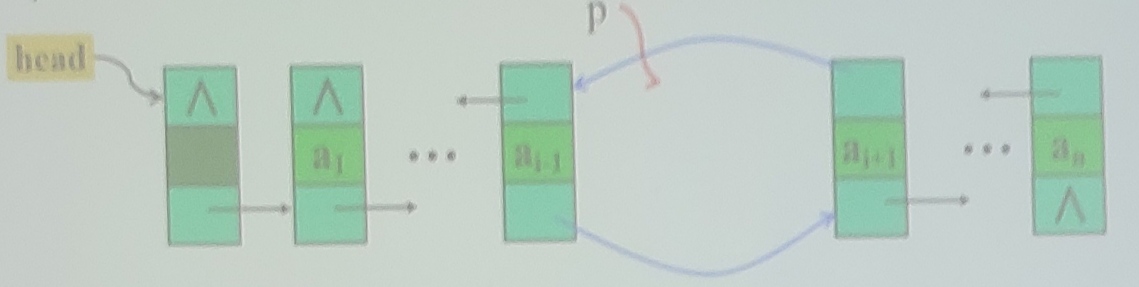
基本步骤
-
定位指针p指向结点$a_i$
-
修改p的前一结点的next指针域指向p下一结点
p->prior->next=p->next; -
修改p的下一结点的prior指针域指向p前一结点
p->next-prior=p->prior; -
释放结点p
用类C语言实现双向循环链表删除
Status ListDelete_DuL(DuLinkList &L,int i,ElemType &e){
//删除带头结点的双链循环线性表L的第i个元素,i的合法值为1<=i<=表长
if(!(p=GetElemP_DuL(L,i))) //在L中确定第i个元素的位置指针p
return ERROR; //P=NULL,即第i个元素不存在
e=p->data;
p->prior->next=p->next;
p->next->prior=p->prior;
free(p);
return OK;
}//ListDelete_DuL
双向循环链表
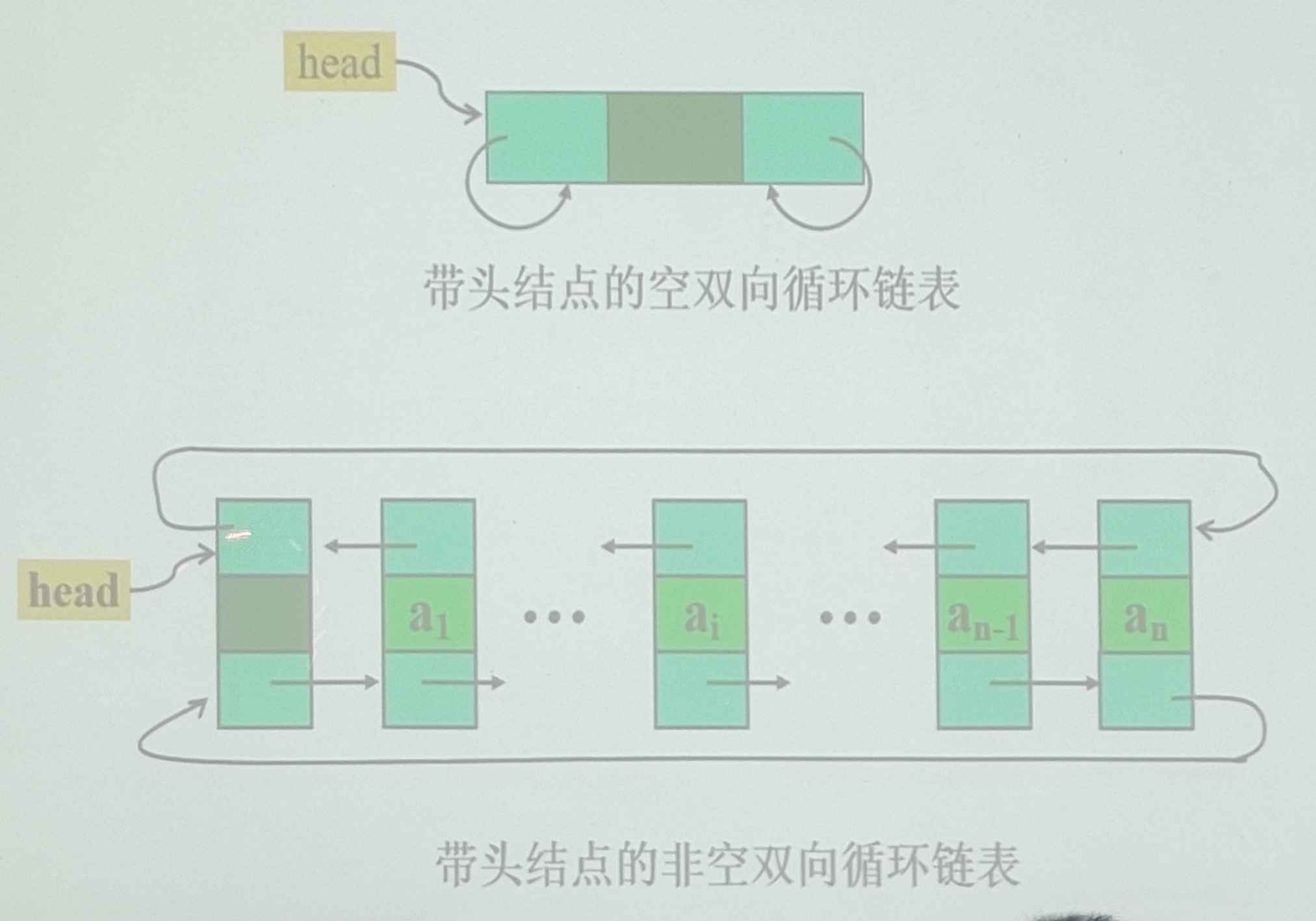
合并线性表
Status MergeList_L(LinkList &La,LinkList &Lb,LinkList &Lc,int(*compare)(ElemType,ElemType)){
//已知单链线性表La和Lb的元素按值非递减排列
//归并La和Lb得到新的单链线性表Lc,Lc的元素也按值非递减排列
if(!InitList(Lc))
return ERROR; //存储空间分配失败
ha=GetHead (La);
hb=GetHead (Lb); ∥ha和hb分别指向La和Lb的头结点
pa=NextPos (La,ha);
pb=NextPos (Lb,hb); ∥pa和pb分别指向La和Lb中当前结点
while(pa&&pb){ ∥La和Lb均非空
a=GetCurElem (pa);
b=GetCurElem (pb); ∥a和b为两表中当前比较元素
if(( * compare) ( a, b) < o){
a<=b;
DelFirst(ha,g);
Append(Lc,g);
pa= NextPos(La,ha);
}else{
a>b;
DelFirst(hb,g);
Append( Lc,q);
pb=NextPos(Lb,hb);
}∥while
if (pa)
Append( Lc, pa); ∥链接La中剩余结点
else
Append(Lc,pb); ∥链接b中剩余结点
FreeNode(ha);
FreeNode (hb); ∥释放La和Lb的头结点
return OK;
}∥MergeList _L
一元多项式的表示及相加
一元多项式的形式
$A(x)=p_0+p_1x+p_2x^2+ \cdots + p_ix^i+p_nx^n$
存储形式
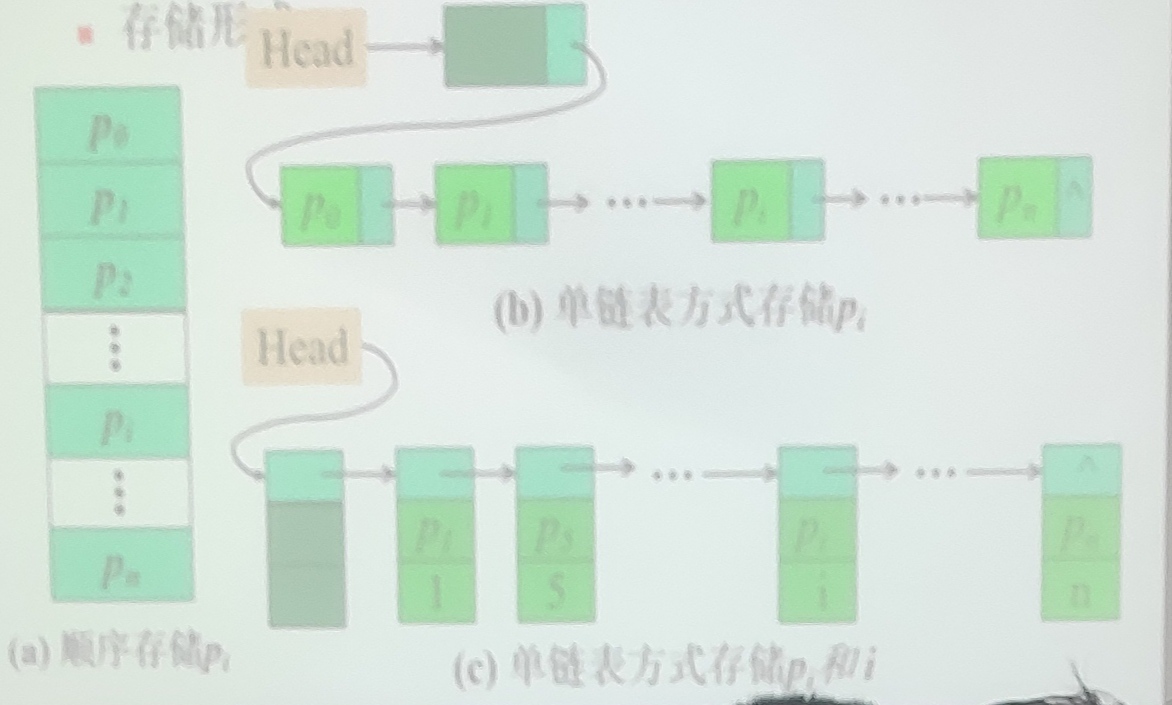
线性表多项式相加
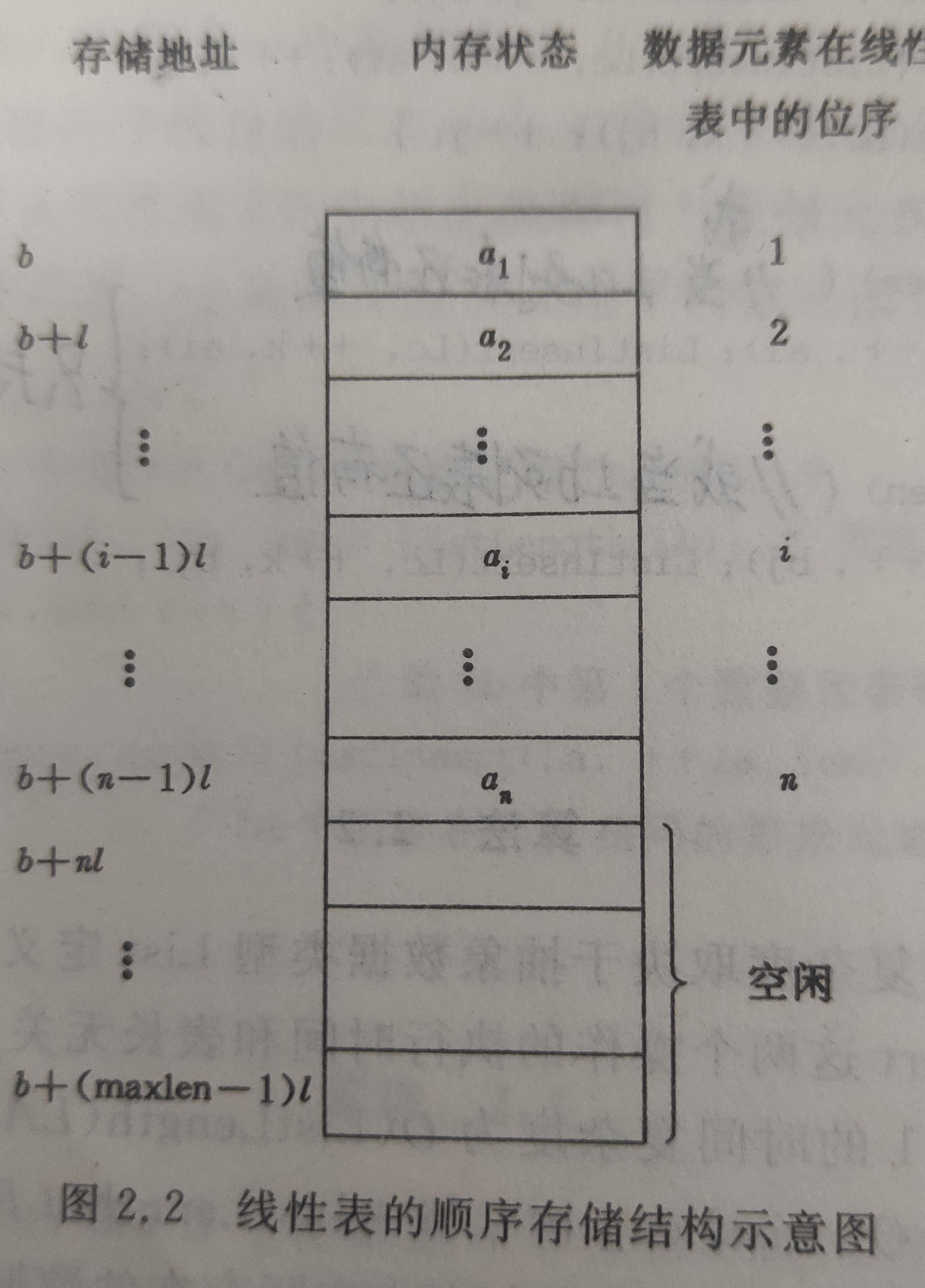
如图,两个线性链表分别表示一元多项式$A_{17}(x)=7+3x+9x^8+5x^{17}$和一元多项式$B_8(x)=8X+22x^7-9x^8$.从图中可见,每个结点表示多项式中的一项
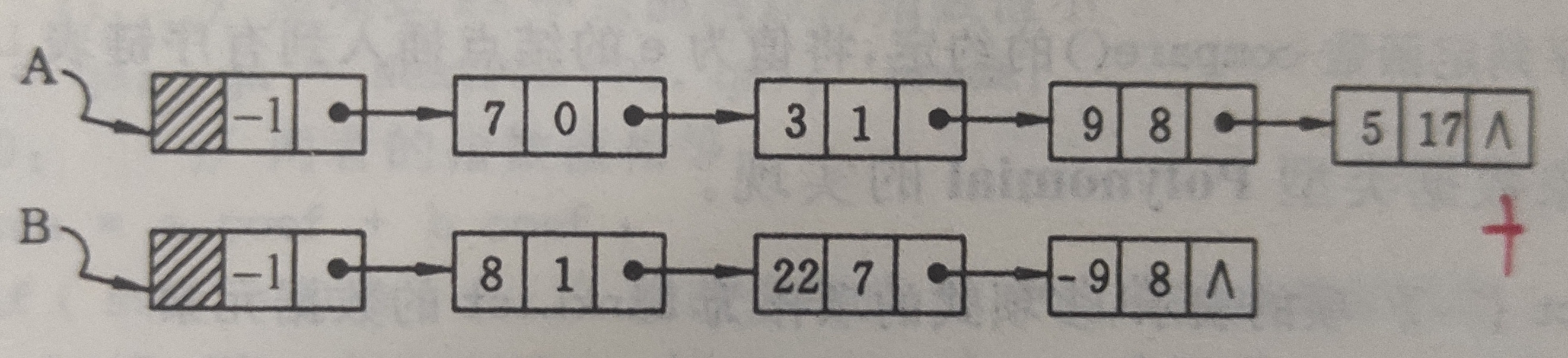
其相加得到: